题目内容
20．已知二元一次方程x-y=2，若y的值大于-3，则x的取值范围是x＞-1．分析 由x-y=2得y=x-2，根据y的值大于-3知x-2＞-3，解之可得．
解答 解：∵由x-y=2得y=x-2，
∴x-2＞-3，
解得：x＞-1，
故答案为：x＞-1．
点评 本题主要考查解一元一次不等式的基本能力，根据题意得出关于x的不等式是关键．
练习册系列答案
阅读快车系列答案
相关题目
，面积相应增加了
，则这个正方形的边长为（ ）
11．适合下列条件的△ABC，直角三角形的个数为（ ）
①a=1，b=2，c=$\sqrt{3}$；
②∠A：∠B：∠C=3：4：5；
③a2-b2=c2；
④∠A+∠B=∠C；
⑤a=$\frac{1}{3}$，b=$\frac{1}{4}$，c=$\frac{1}{5}$．
①a=1，b=2，c=$\sqrt{3}$；
②∠A：∠B：∠C=3：4：5；
③a2-b2=c2；
④∠A+∠B=∠C；
⑤a=$\frac{1}{3}$，b=$\frac{1}{4}$，c=$\frac{1}{5}$．
| A． | 2个 | B． | 3个 | C． | 4个 | D． | 5个 |
电力公司为鼓励市民节约用电，采取按月用电量分段收费办法．若某户居民每月应交电费y（元）与用电量x（度）的函数图象是一条折线（如图所示），根据图象解下列问题：
已知一次函数图象经过点（3，2），（-1，-6）两点．
12．
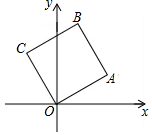如图，点A在第一象限内，其坐标为（2，1），以OA为边在x轴上方作正方形OABC，则正方形OABC的顶点C的坐标是（ ）
如图，点A在第一象限内，其坐标为（2，1），以OA为边在x轴上方作正方形OABC，则正方形OABC的顶点C的坐标是（ ）| A． | （-2，1） | B． | （1，3） | C． | （1，2） | D． | （-1.2） |
7．为了解某种车的耗油量，专业技术人员对这种车在高速公路上做了耗油试验，测得的数据如下表：
（1）根据上表的数据，写出Q与t的关系式Q=100-6t；
（2）汽车行驶5小时后，油箱中的剩余油量是70L；
（3）若汽车油箱中剩余油量为52升，则汽车行使了8小时；
（4）贮满100升汽油的汽车，理论上最多能行驶$\frac{50}{3}$小时．
| 汽车行驶时间t（时） | 0 | 1 | 2 | 3 | … |
| 油箱剩余油量Q（升） | 100 | 94 | 88 | 82 | … |
（2）汽车行驶5小时后，油箱中的剩余油量是70L；
（3）若汽车油箱中剩余油量为52升，则汽车行使了8小时；
（4）贮满100升汽油的汽车，理论上最多能行驶$\frac{50}{3}$小时．