题目内容
若（x-1）7=a0x7+a1x6+a2x5+a3x4+a4x3+a5x2+a6x+a7，则：
（1）a0+a1+a2+a3+a4+a5+a6+a7= ；
（2）a0+a2+a4+a6= ；
（3）a1+a3+a5+a7= ．
（1）a0+a1+a2+a3+a4+a5+a6+a7=
（2）a0+a2+a4+a6=
（3）a1+a3+a5+a7=
考点：代数式求值
专题：
分析：（1）令x=1根据有理数的乘方的定义求解即可；
（2）（3）令x=-1求出-a0+a1-a2+a3-a4+a5-a6+a7的值，然后相加相减分别求解即可．
（2）（3）令x=-1求出-a0+a1-a2+a3-a4+a5-a6+a7的值，然后相加相减分别求解即可．
解答：解：（1）x=1时，a0+a1+a2+a3+a4+a5+a6+a7=（1-1）7=0；
（2）x=-1时，-a0+a1-a2+a3-a4+a5-a6+a7=（-1-1）7=-128，
所以，2（a0+a2+a4+a6）=0-（-128）=128，
所以，a0+a2+a4+a6=64；
（3）2（a1+a3+a5+a7）=0+（-128）=-128，
所以，a1+a3+a5+a7=-64．
故答案为：0；64；-64．
（2）x=-1时，-a0+a1-a2+a3-a4+a5-a6+a7=（-1-1）7=-128，
所以，2（a0+a2+a4+a6）=0-（-128）=128，
所以，a0+a2+a4+a6=64；
（3）2（a1+a3+a5+a7）=0+（-128）=-128，
所以，a1+a3+a5+a7=-64．
故答案为：0；64；-64．
点评：本题考查了代数式求值，x取特殊值并利用整体思想求解是解题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
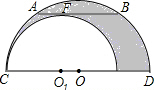如图，大半圆O与小半圆O1相切于点C，大半圆的弦AB与小半圆相切于F，且AB∥CD，AB=4cm，则阴影部分的面积是（ ）| A、πcm2 |
| B、2πcm2 |
| C、3πcm2 |
| D、4πcm2 |
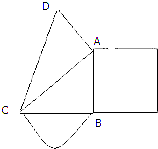如图，Rt△ABC中，以AB为边向外作正方形，以BC为直径向外作半圆，且正方形面积与半圆面积之比为9：2π，现已AC为直角边向外作Rt△ACD，若AD=8，CD=17，则正方形的面积为