题目内容
11. 在平面直角坐标系xOy中,将正比例函数y=-2x的图象沿y轴向上平移4个单位长度后与y轴交于点B,与x轴交于点C.
在平面直角坐标系xOy中,将正比例函数y=-2x的图象沿y轴向上平移4个单位长度后与y轴交于点B,与x轴交于点C.(1)画正比例函数y=-2x的图象,并直接写出直线BC的解析式;
(2)如果一条直线经过点C且与正比例函数y=-2x的图象交于点P(m,2),求m的值及直线CP的解析式.
分析 (1)列表后画出函数的图象即可;根据“上加下减”的原则写出直线BC的解析式;
(2)代入正比例函数解析式求得P的坐标,然后根据直线BC的解析式求得C的坐标,然后根据待定系数法求得即可.
解答 解:(1)列表: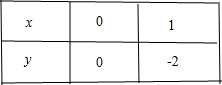
作出函数的图象如图: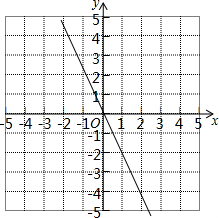
直线BC的解析式为y=-2x+4;
(2)如图,∵直线与正比例函数y=-2x的图象交于点P(m,2),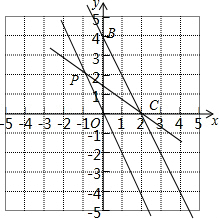
∴2=-2m,解得m=-1,
∴P(-1,2),
∵直线BC与x交于C,
∴C(2,0),
设直线PC的解析式为y=kx+b,
∴$\left\{\begin{array}{l}{-k+b=2}\\{2k+b=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-\frac{2}{3}}\\{b=\frac{4}{3}}\end{array}\right.$,
∴直线CP的解析式为y=-$\frac{2}{3}$x+$\frac{4}{3}$.
点评 本题考查了两条直线平行或相交问题,一次函数的图象与几何变换,待定系数法求一次函数的解析式,熟练掌握待定系数法是解题的关键.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
2.下列判断正确的是( )
| A. | $-\frac{3}{5}$<$-\frac{4}{7}$ | B. | x-2是有理数,它的倒数是$\frac{1}{x-2}$ | ||
| C. | 若|a|=|b|,则a=b | D. | 若|a|=-a,则a<0 |
19.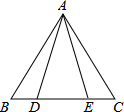 如图,B,D,E,C四点共线,且△ABD≌△ACE,若∠AEC=105°,则∠DAE的度数等于( )
如图,B,D,E,C四点共线,且△ABD≌△ACE,若∠AEC=105°,则∠DAE的度数等于( )
 如图,B,D,E,C四点共线,且△ABD≌△ACE,若∠AEC=105°,则∠DAE的度数等于( )
如图,B,D,E,C四点共线,且△ABD≌△ACE,若∠AEC=105°,则∠DAE的度数等于( )| A. | 30° | B. | 40° | C. | 50° | D. | 65° |
16.在平面直角坐标系中,若点P(a-1,a)在第二象限,则a的取值范围是( )
| A. | a<0 | B. | a>1 | C. | 0<a<1 | D. | -1<a<0 |
3.以3和4为根的一元二次方程是( )
| A. | x2-7x+12=0 | B. | x2+7x+12=0 | C. | x2+7x-12=0 | D. | x2-7x-12=0 |
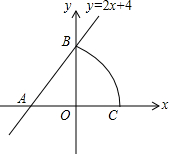 如图,已知直线y=2x+4与x轴交于点A,与y轴交于点B,以点A为圆心,AB为半径画弧,交x轴正半轴于点C,则点C坐标为$(2\sqrt{5}-2,0)$.
如图,已知直线y=2x+4与x轴交于点A,与y轴交于点B,以点A为圆心,AB为半径画弧,交x轴正半轴于点C,则点C坐标为$(2\sqrt{5}-2,0)$. 如图,在平面直角坐标系中,O是坐标原点,二次函数y=x2+c的图象抛物线交x轴于点A,B(点A在点B的左侧),与y轴交于点C(0,-3).
如图,在平面直角坐标系中,O是坐标原点,二次函数y=x2+c的图象抛物线交x轴于点A,B(点A在点B的左侧),与y轴交于点C(0,-3).