Question

20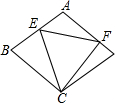．如图，E，F是菱形ABCD边AB与AD上的动点，在点E，F移动的过程中，保持AE=FD，若∠B=60°，AB=4，则△CEF的面积是否存在最小值？如果存在，求出这个值；如果不存在，请说明理由．

Answer 1

分析 首先证明△AFC≌△BEC（SAS）推出CF=CE，△ECF是等边三角形，当CE⊥AB时，CE的长最小，最小值为$\frac{\sqrt{3}}{2}$×6=3$\sqrt{3}$，即可推出△ECF的面积的最小值是$\frac{\sqrt{3}}{4}$•（3$\sqrt{3}$）²；

解答 解：连接CA，如右图所示，
∵四边形ABCD是菱形，∠B=60°，AE=DF，
∴AB=BC=CD=DA，∠BAD=120°，
∴∠FAC=60°，BE=AF，AB=BC=AC，
在△AFC和△BEC中，
$\left\{\begin{array}{l}{AF=BE}\\{∠FAC=∠B}\\{AC=BC}\end{array}\right.$，
∴△AFC≌△BEC（SAS）
∴CF=CE，∠ACF=∠BCE，
又∵∠BCE+∠ECA=60°，
∴∠ECA+∠ACF=60°，
∴△ECF是等边三角形；
当CE⊥AB时，CE的长最小，最小值为$\frac{\sqrt{3}}{2}$×6=3$\sqrt{3}$，
∴△ECF的面积的最小值是$\frac{\sqrt{3}}{4}$•（3$\sqrt{3}$）²=$\frac{27\sqrt{3}}{4}$．

点评 本题考查菱形的性质、最短路线问题、等边三角形的判定和性质、全等三角形的判定和性质等知识，解题的关键是正确寻找全等三角形解决问题，学会利用垂线段最短解决最短问题，属于中考常考题型．