题目内容
16．
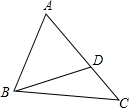如图，D是△ABC的边AC上的一点，连接BD，已知AB=6，AD=4，CD=5．求证：∠ABD=∠C．
分析 先根据题意判断出△ABD∽△ACB，由相似三角形的对应角相等即可得出结论．
解答 证明：∵AB=6，AD=4，CD=5，
∴AC=AD+CD=4+5=9，
∴$\frac{AB}{AC}$=$\frac{6}{9}$=$\frac{2}{3}$，$\frac{AD}{AB}$=$\frac{4}{6}$=$\frac{2}{3}$，
∴$\frac{AB}{AC}$=$\frac{AD}{AB}$．
在△ABD与△ACB中，
∵$\frac{AB}{AC}$=$\frac{AD}{AB}$，∠A=∠A，
∴△ABD∽△ACB，
∴∠ABD=∠C．
点评 本题考查的是相似三角形的判定与性质，熟知相似三角形的对应角相等是解答此题的关键．
练习册系列答案
相关题目
6．下列方程组中，不是二元一次方程组的是（ ）
| A． | $\left\{\begin{array}{l}{3x-2y=0}\\{4x-1=y}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{{x}^{2}-2x=y+{x}^{2}}\\{x+y=8}\end{array}\right.$ | ||
| C． | $\left\{\begin{array}{l}{3x-y=6}\\{x-z=1}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{2x+y=6}\\{2x=y}\end{array}\right.$ |
画出下面几何体从正面、左面、上面看到的图形．
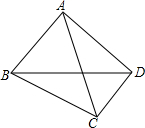如图，四边形ABCD中，∠BAC=∠BCD=90°，若AC平分∠BCD，求证：AB=AD．
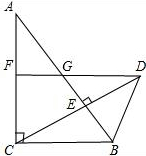如图，在Rt△ABC中，∠ACB=90°，∠A=30°，CD⊥AB交AB于点E，且CD=AC，DF∥BC，分别与AB，AC交于点G，F（说明：在有一个锐角为30°的直角三角形中，30°角所对的直角边长是斜边长的一半．）
看图填空，并在括号内注明说理依据．