题目内容
2．已知两个一次函数y=3x+b1和y=-3x+b2，若b1＜b2＜0，则它们图象的交点在（ ）| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
分析 联立方程组求得$\left\{\begin{array}{l}{x=\frac{{b}_{2}-{b}_{1}}{6}}\\{y=\frac{{b}_{1}+{b}_{2}}{2}}\end{array}\right.$，再由b1＜b2＜0，可得交点的横坐标为正，纵坐标为负．
解答 解：由$\left\{\begin{array}{l}{y=3x+{b}_{1}}\\{y=-3x+{b}_{2}}\end{array}\right.$可得$\left\{\begin{array}{l}{x=\frac{{b}_{2}-{b}_{1}}{6}}\\{y=\frac{{b}_{1}+{b}_{2}}{2}}\end{array}\right.$，
∵b1＜b2＜0，
∴x＞0，y＜0时，交点的横坐标为正，纵坐标为负，即交点在第四象限；
故选：D．
点评 本题主要考查两直线相交或平行的问题及象限内点的坐标特点，掌握根据直线解析式求得交点坐标且各象限内点的坐标特点是解题的关键．
练习册系列答案
优秀生应用题卡口算天天练系列答案
浙江之星课时优化作业系列答案
相关题目
14．
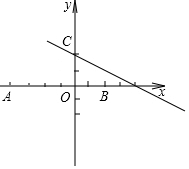如图，已知点A，B的坐标分别为（-4，0）和（2，0），在直线l：y=-$\frac{1}{2}$x+2上取一点C，若△ABC是直角三角形，则满足条件的点C有（ ）
如图，已知点A，B的坐标分别为（-4，0）和（2，0），在直线l：y=-$\frac{1}{2}$x+2上取一点C，若△ABC是直角三角形，则满足条件的点C有（ ）| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
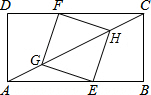如图，矩形ABCD中，AB=8，BC=4，点E在AB上，点F在CD上，点G、H在对角线AC上，若四边形EGFH是正方形，则AG的长是$\sqrt{5}$．
如图，在?ABCD中，E、F分别是AD、CB上任一点，AE≠CF，AB=8，CB=10，S△BOE=6；则S△DOF=6．
11．方程2x2+1=3x的两个根为（ ）
| A． | x1=2，x2=1 | B． | x1=$\frac{1}{2}$，x2=1 | C． | x1=-2，x2=1 | D． | x1=-$\frac{1}{2}$，x2=1 |
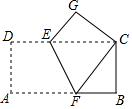如图，已知矩形ABCD，将纸片折叠，使顶点A与C重合，折痕EF分别于DC，AB交于E，F．