Question

12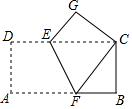．如图，已知矩形ABCD，将纸片折叠，使顶点A与C重合，折痕EF分别于DC，AB交于E，F．
（1）求证：E，A，F，C四点围成的四边形为菱形；
（2）若菱形ABCD中，BC=4，AB=8，求折痕EF的长．

Answer 1

分析 （1）连接AE，AC交EF于O，由折叠的性质得，AO=CO，EF⊥AC，根据全等三角形的性质得到AF=CE，于是得到结论；
（2）根据勾股定理得到AE=5，AC=4$\sqrt{5}$，求得AO=2$\sqrt{5}$，根据全等三角形的性质得到DE=OF，于是得结论．

解答 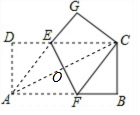解：（1）连接AE，AC交EF于O，
由折叠的性质得，AO=CO，EF⊥AC，
∴AE=CE，AF=CF，
∵AB∥CD，
∴∠ECO=∠OAF，
在△AOF与△COE中，$\left\{\begin{array}{l}{∠OAF=∠OCE}\\{AO=OC}\\{∠AOF=∠COE}\end{array}\right.$，
∴△AOF≌△COE，
∴AF=CE，
∴AE=AF=CE=CF，
∴E，A，F，C四点围成的四边形为菱形；
（2）在Rt△ADE中，AD²+DE²=AE²，即4²+（8-AE）²=AE²，
∴AE=5，
在Rt△ABC中，AB²+BC²=AC²，即8²+4²=AC²，
∴AC=4$\sqrt{5}$，
∴AO=2$\sqrt{5}$，
∵△AOF≌△COE，
∴DE=OF，
∴EF=2DE=2$\sqrt{A{E}^{2}-A{O}^{2}}$=2$\sqrt{5}$．

点评 本题考查了折叠问题：折叠前后两图形全等，即对应线段相等；对应角相等．也考查了勾股定理、菱形的判定方法以及矩形的性质．