题目内容
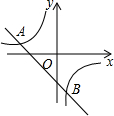 如图,一次函数y=kx+b的图象与反比例函数y=
如图,一次函数y=kx+b的图象与反比例函数y=| m |
| x |
| m |
| x |
| A、-2,2 | B、-1,1 |
| C、-2,1 | D、无法确定 |
考点:反比例函数与一次函数的交点问题
专题:
分析:把点A的坐标代入y=
得出反比例函数关系式,把B的纵坐标代入,求出B点的横坐标,根据图形得出x的解.
| m |
| x |
解答:解:∵A的坐标为(-2,1),
∴1=
,解得m=-2,
∴y=
,
∵B的纵坐标为-2,
∴-2=
,解得x=1,
∴点B(1,-2),
根据图象信息可得关于x的方程kx+b=
的解为点A,B的横坐标,即-2,1.
故选:C.
∴1=
| m |
| -2 |
∴y=
| -2 |
| x |
∵B的纵坐标为-2,
∴-2=
| -2 |
| x |
∴点B(1,-2),
根据图象信息可得关于x的方程kx+b=
| m |
| x |
故选:C.
点评:本题主要考查了反比例函数与一次函数的交点.解题的关键是求出点B的坐标.

练习册系列答案
相关题目
根据下列表格中的对应值,判断方程ax2+bx+c=0(a≠0,a,b,c为常数)的根的个数是( )
| x | 6.17 | 6.18 | 6.19 | 6.20 |
| y=ax2+bx+c | 0.02 | -0.01 | 0.02 | 0.04 |
| A、0 | B、1 | C、2 | D、1或2 |
如果
是二次根式,那么x应满足的条件是( )
|
| A、x≠2的实数 |
| B、x<2的实数 |
| C、x>2的实数 |
| D、x>0且x≠2的实数 |
如果不等式组
恰有3个整数解,则a的取值范围是( )
|
| A、a≤-1 |
| B、a<-1 |
| C、-2≤a<-1 |
| D、-2<a≤-1 |