题目内容
某电子产品生产车间工人20名,已知每名工人每天可生产甲种产品12个或乙种产品10个.且每生产一个甲种产品可获得利润50元,每生产一个乙种产品可获得利润80元.在这20名工人中,车间每天安排x名工人生产甲种产品,其余工人生产乙种产品.
(1)请写出此车间每天获取利润y(元)与x(人)之间的函数关系式;
(2)若要使此车间每天获取利润为14000元,要派多少名工人去生产甲种产品?
(3)若要使此车间每天获取利润不低于14600元,你认为至少要派多少名工人去生产乙种产品才合适?
(1)请写出此车间每天获取利润y(元)与x(人)之间的函数关系式;
(2)若要使此车间每天获取利润为14000元,要派多少名工人去生产甲种产品?
(3)若要使此车间每天获取利润不低于14600元,你认为至少要派多少名工人去生产乙种产品才合适?
考点:一次函数的应用
专题:
分析:(1)根据每个工人每天生产的产品个数以及每个产品的利润,表示出总利润即可;
(2)根据每天获取利润为14400元,则y=14400,求出即可;
(3)根据每天获取利润不低于14600元即y≥14600,求出即可.
(2)根据每天获取利润为14400元,则y=14400,求出即可;
(3)根据每天获取利润不低于14600元即y≥14600,求出即可.
解答:解:(1)根据题意得:y=12x×50+10(20-x)×80=-200x+16000;
(2)当y=14000时,有14400=-200x+16000,
解得:x=10,
故要拍10名工人去生产甲种产品;
(3)根据题意得:y≥14600,即-200x+16000≥14600,
解得:x≤7,
则20-x≥13,
故至少要拍13名工人去生产乙中产品才合适.
(2)当y=14000时,有14400=-200x+16000,
解得:x=10,
故要拍10名工人去生产甲种产品;
(3)根据题意得:y≥14600,即-200x+16000≥14600,
解得:x≤7,
则20-x≥13,
故至少要拍13名工人去生产乙中产品才合适.
点评:此题主要考查了一次函数的应用以及一元一次不等式的应用等知识,根据已知得出y与x之间的函数关系是解题关键.

练习册系列答案
相关题目
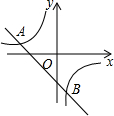 如图,一次函数y=kx+b的图象与反比例函数y=
如图,一次函数y=kx+b的图象与反比例函数y=| m |
| x |
| m |
| x |
| A、-2,2 | B、-1,1 |
| C、-2,1 | D、无法确定 |
下列方程中,解为x=2的方程是( )
| A、3x-2=3 | ||
| B、4-2(x-1)=1 | ||
| C、6-x=2x | ||
D、
|
下面有4个汽车标志图案,其中是轴对称图形的有( )


| A、1个 | B、2个 | C、3个 | D、4个 |
 如图,直线y=kx+b交坐标轴于A(-2,0),B(0,3)两点,则不等式kx+b>0的解集
如图,直线y=kx+b交坐标轴于A(-2,0),B(0,3)两点,则不等式kx+b>0的解集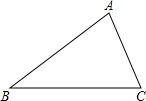 如图,已知△ABC(AB>AC).
如图,已知△ABC(AB>AC).