题目内容
12.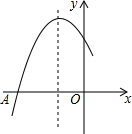 如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为直线x=-1,给出四个结论:
如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为直线x=-1,给出四个结论:①b2>4ac;②2a+b=0;③a+b+c>0;④若点B(-$\frac{5}{2}$,y1)、C(-$\frac{1}{2}$,y2)为函数图象上的两点,则y1<y2,
其中正确结论是( )
| A. | ②④ | B. | ①④ | C. | ①③ | D. | ②③ |
分析 由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
解答 解:∵抛物线的开口方向向下,
∴a<0;
∵抛物线与x轴有两个交点,
∴b2-4ac>0,即b2>4ac,
故①正确
由图象可知:对称轴x=-$\frac{b}{2a}$=-1,
∴2a-b=0,
故②错误;
∵抛物线与y轴的交点在y轴的正半轴上,
∴c>0
由图象可知:当x=1时y=0,
∴a+b+c=0;
故③错误;
由图象可知:若点B(-$\frac{5}{2}$,y1)、C(-$\frac{1}{2}$,y2)为函数图象上的两点,则y1<y2,
故④正确.
故选B
点评 此题考查二次函数的性质,解答本题关键是掌握二次函数y=ax2+bx+c系数符号由抛物线开口方向、对称轴、抛物线与y轴的交点、抛物线与x轴交点的个数确定.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
3.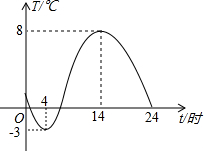 如图,是一台自动测温记录仪的图象,它反映了我市冬季某天气温T随时间t变化而变化的关系,观察图象得到下列信息,其中错误的是( )
如图,是一台自动测温记录仪的图象,它反映了我市冬季某天气温T随时间t变化而变化的关系,观察图象得到下列信息,其中错误的是( )
 如图,是一台自动测温记录仪的图象,它反映了我市冬季某天气温T随时间t变化而变化的关系,观察图象得到下列信息,其中错误的是( )
如图,是一台自动测温记录仪的图象,它反映了我市冬季某天气温T随时间t变化而变化的关系,观察图象得到下列信息,其中错误的是( )| A. | 凌晨4时气温最低为-3℃ | |
| B. | 14时气温最高为8℃ | |
| C. | 从0时至14时,气温随时间增长而上升 | |
| D. | 从14时至24时,气温随时间增长而下降 |
20.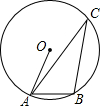 如图,A,B,C是⊙O上三点,∠ACB=25°,则∠BAO的度数是( )
如图,A,B,C是⊙O上三点,∠ACB=25°,则∠BAO的度数是( )
 如图,A,B,C是⊙O上三点,∠ACB=25°,则∠BAO的度数是( )
如图,A,B,C是⊙O上三点,∠ACB=25°,则∠BAO的度数是( )| A. | 55° | B. | 60° | C. | 65° | D. | 70° |
 如图,P为线段AB上一点,AD与BC交于点E,∠CPD=∠A=∠B,BC交PD于点F,AD交PC于点G,则图中相似三角形有3对.
如图,P为线段AB上一点,AD与BC交于点E,∠CPD=∠A=∠B,BC交PD于点F,AD交PC于点G,则图中相似三角形有3对. 如图,在△ABC中,DE∥BC,AD:DB=1:2,DE=2,则BC的长是6.
如图,在△ABC中,DE∥BC,AD:DB=1:2,DE=2,则BC的长是6. 一块直角三角板ABC按如图放置,顶点A的坐标为(0,1),直角顶点C的坐标为(-3,0),∠B=30°,则点B的坐标为(-3-$\sqrt{3}$,3$\sqrt{3}$).
一块直角三角板ABC按如图放置,顶点A的坐标为(0,1),直角顶点C的坐标为(-3,0),∠B=30°,则点B的坐标为(-3-$\sqrt{3}$,3$\sqrt{3}$).
 选作题(请从以下两个小题中任选一题作答,若多选,则按所选的第一题计分.)
选作题(请从以下两个小题中任选一题作答,若多选,则按所选的第一题计分.)