题目内容
2．
如图，P为线段AB上一点，AD与BC交于点E，∠CPD=∠A=∠B，BC交PD于点F，AD交PC于点G，则图中相似三角形有3对．
分析 先根据条件证明△PCF∽△BCP，利用相似三角形的性质：对应角相等，再证明△APD∽△PGD，进而证明△APG∽△BFP再证明时注意图形中隐含的相等的角．
解答 解：∵∠CPD=∠B，∠C=∠C，
∴△PCF∽△BCP．
∵∠CPD=∠A，∠D=∠D，
∴△APD∽△PGD．
∵∠CPD=∠A=∠B，∠APG=∠B+∠C，∠BFP=∠CPD+∠C
∴∠APG=∠BFP，
∴△APG∽△BFP．
则图中相似三角形有3对，
故答案为：3．
点评 本题考查相似三角形的判定．识别两三角形相似，除了要掌握定义外，还要注意正确找出两三角形的对应边、对应角．
练习册系列答案
相关题目
12．-$\frac{2}{5}$的绝对值是（ ）
| A． | $\frac{5}{2}$ | B． | -$\frac{5}{2}$ | C． | $\frac{2}{5}$ | D． | -$\frac{2}{5}$ |
二次函数y=ax2+bx+c（a≠0）的图象如图，若|ax2+bx+c|=k（k≠0）有两个不相等的实数根，则k的取值范围是k＞3．
“综合与实践”学习活动准备制作一组三角形，记这些三角形的三边分别为a，b，c，并且这些三角形三边的长度为大于1且小于5的整数个单位长度．
7．下列说法中正确的是（ ）
| A． | 在统计学中，把组成总体的每一个考察对象叫做样本容量 | |
| B． | 为了解全国中学生的心理健康情况，应该采用普查的方式 | |
| C． | 一组数据6，8，7，8，8，9，10的众数和中位数都是8 | |
| D． | 若甲组数据的方差为s12=0.4，乙组数据的方差为s12=0.05，则甲组数据更稳定 |
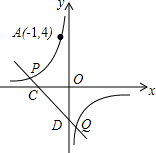如图，反比例函数y=$\frac{k}{x}$的图象经过点A（-1，4），直线y=-x+b（b≠0）与双曲线y=$\frac{k}{x}$在第二、四象限分别相交于P，Q两点，与x轴、y轴分别相交于C，D两点．
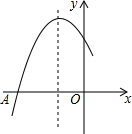如图是二次函数y=ax2+bx+c图象的一部分，图象过点A（-3，0），对称轴为直线x=-1，给出四个结论：