题目内容
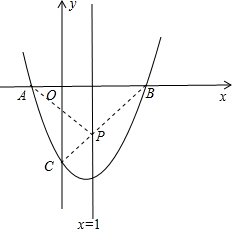
11.二次函数y=x2-2x-3的图象与x轴从左到右两个交点依次为A、B,与y轴交于点C.(1)求A、B、C三点的坐标;
(2)如果P是该抛物线对称轴上一点,试求出使PA+PC最小的点P的坐标.
分析 (1)根据抛物线与x轴的交点问题,通过解方程x2-2x-3=0即可得到A点和B点坐标,然后求当x=0时的函数值即可得到C点坐标;
(2)利用抛物线的对称性可得抛物线的对称轴为直线x=1,连结BC交直线x=1于P点,利用两点之间线段最短可判断此时的点P使PA+PC最小,接着利用待定系数法求出直线BC的解析式,然后求直线BC与直线x=1的交点坐标即可.
解答 解:(1)令y=0,即x2-2x-3=0,解得x1=-1,x2=-3,
∴A(-1,0),B(3,0),
当x=0时,y=x2-2x-3=-3,
∴C(0,-3);
(2) ∵A(-1,0),B(3,0),
∵A(-1,0),B(3,0),
∴抛物线的对称轴为直线x=1,
连结BC交直线x=1于P点,
∵PA=PB,
∴PA+PC=PB+PC=BC,
∴点P使PA+PC最小,
设直线BC的解析式为y=kx+b,
把B(3,0),C(0,-3)代入得$\left\{\begin{array}{l}{3k+b=0}\\{b=-3}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=1}\\{b=3}\end{array}\right.$,
∴直线BC的解析式为y=x-3,
当x=1时,y=x-3=1-3=-2,
∴P点坐标为(1,-2).
点评 本题考查了抛物线与x轴的交点问题:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标转化为解关于x的一元二次方程.也考查了关于最短路径问题的解决方法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,点D,E在线段BC上,且△ABC是等边三角形,当DB,BC,CE满足怎样的关系时,△ADB∽△EAC,并加以证明.
如图,点D,E在线段BC上,且△ABC是等边三角形,当DB,BC,CE满足怎样的关系时,△ADB∽△EAC,并加以证明.