题目内容
16.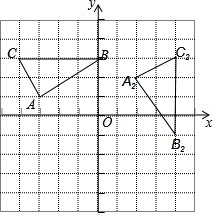 如图,平面直角坐标系中,已知A(-3,1)、B(0,3)、C(-4,3).
如图,平面直角坐标系中,已知A(-3,1)、B(0,3)、C(-4,3).(1)将△ABC经过平移后得到△A1B1C1,若点C1的坐标为(0,-1),在图中画出△A1B1C1;
(2)顶点A1坐标为(1,-3),B1的坐标为(4,-1);
(3)将△ABC绕点P沿顺时针方向旋转后得到△A2B2C2,则点P的坐标是(0,-1),旋转角的度数是90°.
分析 (1)根据C点和C1点的坐标得出规律,再画出图形即可;
(2)根据图象得出即可;
(3)根据两三角形的顶点的坐标,即可得出答案.
解答 解:(1)如图所示:△A1B1C1: ;
;
(2)顶点A1坐标为(1,-3),B1的坐标为(4,-1),
故答案为:(1,-3),(4,-1);
(3)∵从图象可知:A(-3,1),B(0,3),C(-4,-3),A2(2,2),B2(4,-1),C2(4,3),
∴将△ABC绕点P沿顺时针方向旋转后得到△A2B2C2,则点P的坐标是(0,-1),旋转角的度数是90°,
故答案为:(0,-1),90°.
点评 本题考查了平移的性质和旋转的性质,能正确读出各个点的坐标是解此题的关键.

练习册系列答案
相关题目
9.下列整式中,属于多项式的是( )
| A. | a-2b | B. | -2ab | C. | -2 | D. | a |
8.下列说法不正确的是( )
| A. | $\frac{1}{25}$的平方根是±$\frac{1}{5}$ | B. | -9是81的一个平方根 | ||
| C. | 0.2的算术平方根是0.01 | D. | -27的立方根是-3 |
5.“抛掷图钉实验”的结果如下:
由表可知,“针尖不着地的”的概率的估计值是0.61.
| 抛掷次数n | 100 | 200 | 300 | 400 | 600 | 800 | 1000 |
| 针尖不着地的频数m | 64 | 118 | 189 | 252 | 360 | 488 | 610 |
| 针尖不着地的频数$\frac{m}{n}$ | 0.64 | 0.59 | 0.63 | 0.63 | 0.60 | 0.61 | 0.61 |
3.若a<b,则下列各式错误的是( )
| A. | a-3<b-3 | B. | -2a<-2b | C. | 0.7a<0.7b | D. | -$\frac{a}{4}$$>-\frac{b}{4}$ |
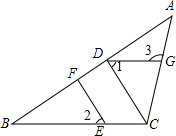 如图,在△ABC中,DG∥BC,∠1=∠2.
如图,在△ABC中,DG∥BC,∠1=∠2.