题目内容
邻补角的角平分线所在的两条直线互相垂直。 （___）
√
【解析】试题分析：邻补角的角平分线所在的两条直线互相垂直，故本题答案为“√”．
练习册系列答案
相关题目
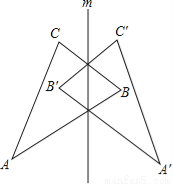
如图，△ABC和△A′B′C′关于直线m对称．
（1）结合图形指出对称点．
（2）连接A、A′，直线m与线段AA′有什么关系？
（3）延长线段AC与A′C′，它们的交点与直线m有怎样的关系？其它对应线段（或其延长线）的交点呢？你发现了什么规律，请叙述出来与同伴交流．
【解析】
（1）对称点有A和A'，B和B'，C和C'．
（2）连接A、A′，直线m是线段AA′的垂直平分线．
（3）延长线段AC与A′C′，它们的交点在直线m上，其它对应线段（或其延长线）的交点也在直线m上，
即若两线段关于直线m对称，且不平行，则它们的交点或它们的延长线的交点在对称轴上．
【解析】本题考查轴对称图形的定义，如果一个图形沿着一条直线对折，两侧的图形能完全重... 如图，图形是由棋子围成的正方形图案，图案的每条边有4个棋子，这个图案有_________条对称轴.
4
【解析】【解析】
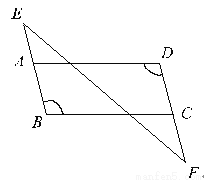
作为一个正方形，其对称轴只有四条．故答案为：4． 已知：如图，BE∥DF，∠B=∠D。求证：AD∥BC。
证明见解析
【解析】试题分析：根据BE∥DF得出∠D=∠EAD，结合已知条件得出∠B=∠EAD，从而根据同位角相等两直线平行得出答案．
试题解析：∵BE∥DF（已知），∴∠D=∠EAD（两条直线平行，内错角相等），
∵∠B=∠D（已知），∴∠B=∠EAD，∴AD∥BC（同位角相等，两直线平行）． 如图，如果AB∥CD，CD∥EF，那么∠BCE等于（ ）
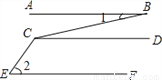
A. ∠1＋∠2 B. ∠2－∠1 C. 180°－∠2＋∠1 D. 180°－∠1＋∠2
C
【解析】试题分析：根据AB∥CD可得：∠BCD=∠1；根据CD∥EF可得：∠2+∠DCE=180°，则∠DCE=180°-∠2，则∠BCE=∠BCD+∠DCE=∠1+180°-∠2，故选C． 和为180的两个角是邻补角。 （___）
×
【解析】试题分析：两个角有一条公共边，它们的另一条边互为反向延长线，具有这种关系的两个角叫做邻补角，故本题答案为“×”． 在函数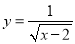
中，自变量x的取值范围是 ．
x＞2．
【解析】试题分析：由题意得，x﹣2＞0，
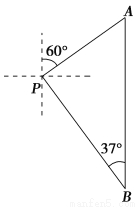
解得x＞2． 周末，小亮一家在东昌湖游玩，妈妈在湖心岛岸边P处观看小亮与爸爸在湖中划船（如图）.小船从P处出发，沿北偏东60°划行200米到达A处，接着向正南方向划行一段时间到达B处.在B处小亮观测妈妈所在的P处在北偏西37°方向上，这时小亮与妈妈相距多少米（精确到米）？（参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75，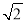
≈1.41，
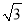≈1.73）
288米
【解析】
【解析】
作PD⊥AB于点D，
由已知得PA＝200米，∠APD＝30°，∠B＝37°，
在Rt△PAD中，
由cos30°＝，得PD＝PAcos30°＝200×＝100米，
在Rt△PBD中，由sin37°＝，
得PB＝≈≈288米.
答：小亮与妈妈的距离约为288米. 在△ABC中，∠A－∠B=30°、∠C=4∠B，则∠C=________．
100°
【解析】试题解析：
①，
②，
①?②得, 解得
故答案为：