题目内容
1.材料:相似三角形的对应边的比相等,对应角相等.(1)如图①,△ABC中,∠A=50°,∠B=45°,点D、E分别在AB、AC上,且AD•AB=AE•AC.则△ABC与△ADE的关系为△ABC∽△AED,∠ADE=85°;
(2)如图②,在平行四边形ABCD中,对角线AC、BD交于点O,M为AD中点,连接CM交BD于点N,且ON=1,求BD的长;
(3)△ABC中,∠A=25°,CD是边AB上的高,且CD2=AD•BD,请直接写出∠ABC的度数.
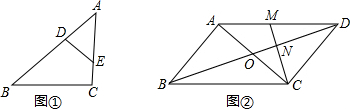
分析 (1)如图①,由AD•AB=AE•AC可推出△ABC∽△AED,从而得到∠ADE=∠C,再根据三角形的内角和定理就可解决问题;
(2)如图②,易证△MND∽△CNB,则有$\frac{MD}{CB}$=$\frac{DN}{BN}$,由M为AD中点及AD=BC可得BN=2DN.设OB=OD=x,则有BD=2x,BN=OB+ON=x+1,DN=x-1,从而可得x+1=2(x-1),求出x就可解决问题;
(3)由于CD的位置不确定,故需分情况讨论.由CD2=AD•BD可证到△DAC∽△DCB,则有∠DCB=∠A=25°,然后利用三角形的内角和定理及外角的性质就可解决问题.
解答 解:(1)答案为△ABC∽△AED,∠ADE=85°.
提示:如图①,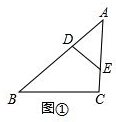
∵AD•AB=AE•AC,
∴$\frac{AB}{AE}$=$\frac{AC}{AD}$.
∵∠A=∠A,
∴△ABC∽△AEB,
∴∠ADE=∠C.
∵∠A=50°,∠B=45°,
∴∠C=180°-50°-45°=85°,
∴∠ADE=85°;
(2)如图②,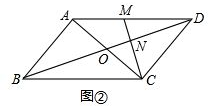
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,OB=OD,
∴∠DMN=∠BCN,∠MDN=∠NBC,
∴△MND∽△CNB,
∴$\frac{MD}{CB}$=$\frac{DN}{BN}$.
∵M为AD中点,
∴MD=$\frac{1}{2}$AD=$\frac{1}{2}$BC,即$\frac{MD}{CB}$=$\frac{1}{2}$,
∴$\frac{DN}{BN}$=$\frac{1}{2}$,即BN=2DN.
设OB=OD=x,则有BD=2x,BN=OB+ON=x+1,DN=x-1,
∴x+1=2(x-1),
解得x=3.
∴BD=2x=6;
(3)∠ABC的度数为65°或115°.
提示:CD可能在△ABC内,如图③,也可能在△ABC外,如图④.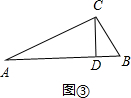
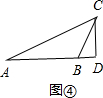
由CD2=AD•BD可证到△DAC∽△DCB,
从而得到∠DCB=∠A=25°,
如图③,∠B=90°-25°=65°,
如图④,∠ABC=90°+25°=115°.
点评 本题主要考查了相似三角形的判定与性质、平行四边形的性质、三角形的内角和定理、三角形外角性质等知识,由于三角形高的位置与三角形的形状有关,当三角形的形状不确定时,常需分类讨论.

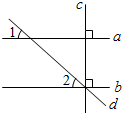 如图,直线a,b,c,d,已知c⊥a,c⊥b,直线b,c,d交于一点,若∠1=60°,则∠2等于( )
如图,直线a,b,c,d,已知c⊥a,c⊥b,直线b,c,d交于一点,若∠1=60°,则∠2等于( )| A. | 60° | B. | 50° | C. | 40° | D. | 30° |
| A. | 三角形和四边形都具有稳定性 | |
| B. | 三角形的稳定性 | |
| C. | 四边形的不稳定性 | |
| D. | 三角形的稳定性和四边形的不稳定性 |
 如图,AB是⊙O的直径,C是半圆上的一个三等分点,D是$\widehat{AC}$的中点,P是直径AB上一点,⊙O是半径为1,则PC+PD的最小值是$\sqrt{2}$.
如图,AB是⊙O的直径,C是半圆上的一个三等分点,D是$\widehat{AC}$的中点,P是直径AB上一点,⊙O是半径为1,则PC+PD的最小值是$\sqrt{2}$.
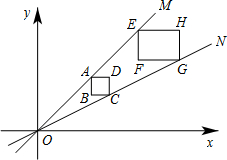 正方形ABCD,矩形EFGH均位于第一象限内,它们的边平行于x轴或y轴,其中,点A,E在直线OM上,点C,G在直线ON上,O为坐标原点,点A的坐标为(3,3),正方形ABCD的边长为1.若矩形EFGH的周长为10,面积为6,则点F的坐标为(7,5),(8,5).
正方形ABCD,矩形EFGH均位于第一象限内,它们的边平行于x轴或y轴,其中,点A,E在直线OM上,点C,G在直线ON上,O为坐标原点,点A的坐标为(3,3),正方形ABCD的边长为1.若矩形EFGH的周长为10,面积为6,则点F的坐标为(7,5),(8,5).