题目内容
 如图,在等边△ABC边上取中点D,BC延长线取一点E,使得CE=CD,DF⊥BE,AB=a.
如图,在等边△ABC边上取中点D,BC延长线取一点E,使得CE=CD,DF⊥BE,AB=a.(1)求证:BD=DE;
(2)求BF的长.
考点:等边三角形的性质,勾股定理
专题:
分析:(1)根据等边三角形的性质得到∠DBC=30°,∠ACB=60°,再根据角之间的关系可得到∠DBC=∠E=30°,即BD=DE.
(2)通过解直角三角形即可求得.
(2)通过解直角三角形即可求得.
解答:证明:(1)在等边△ABC中,
∴∠ACB=60°,AB=BC,∠ABC=60°,
∵D为AC的中点,
∴∠DBC=
∠ABC=
×60°=30°,
∵DC=CE,
∴∠E=∠CDE.
∵∠ACB=∠E+∠EDC=60°,
∴∠E=∠CDE=30°.
∴∠DBC=∠DEC=30°.
∴BD=DE.
(2)∵在等边△ABC中,D为AC的中点,
∴BD⊥AC,
∴BD=AB•sin60°=
a,
∵DF⊥BE,
∴BF=BD•cos30°=
×
a=
a.
∴∠ACB=60°,AB=BC,∠ABC=60°,
∵D为AC的中点,
∴∠DBC=
| 1 |
| 2 |
| 1 |
| 2 |
∵DC=CE,
∴∠E=∠CDE.
∵∠ACB=∠E+∠EDC=60°,
∴∠E=∠CDE=30°.
∴∠DBC=∠DEC=30°.
∴BD=DE.
(2)∵在等边△ABC中,D为AC的中点,
∴BD⊥AC,
∴BD=AB•sin60°=
| ||
| 2 |
∵DF⊥BE,
∴BF=BD•cos30°=
| ||
| 2 |
| ||
| 2 |
| 3 |
| 4 |
点评:此题主要考查学生对等边三角形的性质的理解及运用,应用直角三角函数解直角三角形;进行角的等量代换是正确解答本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
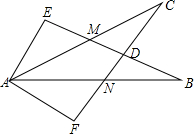 如图,已知∠E=∠F=90°,∠EAM=∠FAN,AE=AF,求证:CM=BN.
如图,已知∠E=∠F=90°,∠EAM=∠FAN,AE=AF,求证:CM=BN.