题目内容
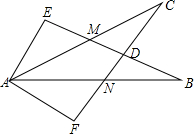 如图,已知∠E=∠F=90°,∠EAM=∠FAN,AE=AF,求证:CM=BN.
如图,已知∠E=∠F=90°,∠EAM=∠FAN,AE=AF,求证:CM=BN.考点:全等三角形的判定与性质
专题:证明题
分析:根据ASA,可得△AEM与△AFN的关系,根据全等三角形的性质,可得AM与AN的关系,根据等式的性质,可得∠EAB与∠FAC的关系,根据ASA,可得△AEB与△AFC的关系,根据全等三角形的性质,可得AC与AB的关系,根据等式的性质,可得答案.
解答:证明:在△AEM和△AFN中,
,
∴△AEM≌△AFN(SAS),
∴AM=AN.
∵∠EAM=∠FAN,
∴∠EAM+∠MAB=∠FAN+∠MAB,
即∠EAB=∠FAC.
在△EAB和△FAC中,
,
∴△EAB≌△FAC(SAS),
∴AB=AC.
∵AB-AN=AC-AM,
∴CM=BN.
|
∴△AEM≌△AFN(SAS),
∴AM=AN.
∵∠EAM=∠FAN,
∴∠EAM+∠MAB=∠FAN+∠MAB,
即∠EAB=∠FAC.
在△EAB和△FAC中,
|
∴△EAB≌△FAC(SAS),
∴AB=AC.
∵AB-AN=AC-AM,
∴CM=BN.
点评:本题考查了全等三角形的判定与性质,利用了全等三角形的判定与性质,等式的性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,AD是△ABC的外角平分线,CD⊥AD于D,E是BC的中点.求证:
如图,AD是△ABC的外角平分线,CD⊥AD于D,E是BC的中点.求证: 如图,在等边△ABC边上取中点D,BC延长线取一点E,使得CE=CD,DF⊥BE,AB=a.
如图,在等边△ABC边上取中点D,BC延长线取一点E,使得CE=CD,DF⊥BE,AB=a.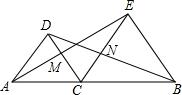 如图,△DAC和△EBC均是等边三角形,AE、BD分别与CD、CE交于点M、N,有如下结论:①△ACE≌△DCB;②△ACM≌△DCN;③CM=CN.其中,正确的是
如图,△DAC和△EBC均是等边三角形,AE、BD分别与CD、CE交于点M、N,有如下结论:①△ACE≌△DCB;②△ACM≌△DCN;③CM=CN.其中,正确的是