题目内容
4.已知锐角三角形ABC的三个内角A、B、C满足:A>B>C,用a表示A-B,B-C以及90°-A中的最小者,则a的最大值为15°.分析 先根据条件得出A-B≥α,B-C≥α,90°-A≥α,将此三个式子利用不等式的性质进行化简,最后用三角形的内角和定理即可得出结论.
解答 解:∵a表示A-B,B-C以及90°-A中的最小者,
∴A-B≥α,B-C≥α,90°-A≥α,
∴2(A-B)≥2α,3(90°-A)≥3α,
∴2(A-B)+(B-C)+3(90°-A)≥2α+α+3α,
∴270°-(A+B+C)≥6α,
∵锐角三角形ABC的三个内角A、B、C,
∴A+B+C=180°,
∴6α≤90°,
∴α≤15°,
而当A-B=B-C=90°-A=15°,得
A=75°,B=60°,C=45°,满足题设条件,
所以,α可取得最大值15°,
故答案为15°.
点评 此题主要考查了不等式的性质,三角形的内角和定理,解本题的关键是得出A-B≥α,B-C≥α,90°-A≥α,难点是这三个式子的处理.

练习册系列答案
相关题目
 如图,点O是直线EP上一点,射线OA,OB,OC在直线EF的上方,射线OD在直线EF的下方,且OF平分∠COD,OA⊥OC,OB⊥OD.
如图,点O是直线EP上一点,射线OA,OB,OC在直线EF的上方,射线OD在直线EF的下方,且OF平分∠COD,OA⊥OC,OB⊥OD. 如图,正方形ABCD的顶点A的坐标为(0,3),顶点B在轴的正方向上,tan∠OBA=3,对角线AC,BD交于点P,射线OP交AB于点N,交DC于点M,点R从O出发沿OM方向以每秒$\sqrt{2}$个单位的速度运动,运动时间为t.
如图,正方形ABCD的顶点A的坐标为(0,3),顶点B在轴的正方向上,tan∠OBA=3,对角线AC,BD交于点P,射线OP交AB于点N,交DC于点M,点R从O出发沿OM方向以每秒$\sqrt{2}$个单位的速度运动,运动时间为t.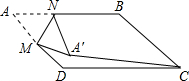 如图,?ABCD中,AB=2$\sqrt{2}$,BC=2,∠B=135°,M是AD边的中点,N是AB边上的一动点,将△AMN沿MN所在直线翻折得到△A′MN,连接A′C,则A′C长度的最小值是$\sqrt{13}$-1.
如图,?ABCD中,AB=2$\sqrt{2}$,BC=2,∠B=135°,M是AD边的中点,N是AB边上的一动点,将△AMN沿MN所在直线翻折得到△A′MN,连接A′C,则A′C长度的最小值是$\sqrt{13}$-1.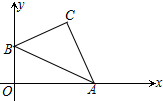 在平面直角坐标系中,已知点A、B的坐标分别为A(6,0)、B(0,2),以AB为斜边在右上方作Rt△ABC.设点C坐标为(x,y),则(x+y)的最大值=4+2$\sqrt{5}$.
在平面直角坐标系中,已知点A、B的坐标分别为A(6,0)、B(0,2),以AB为斜边在右上方作Rt△ABC.设点C坐标为(x,y),则(x+y)的最大值=4+2$\sqrt{5}$.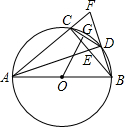 如图,⊙O是Rt△ABC的外接圆,AC=BC,∠CAB的平分线AD交BC于点E、交⊙O于点D,延长BD交AC的延长线线于点F,连结CD、OG平分CD.
如图,⊙O是Rt△ABC的外接圆,AC=BC,∠CAB的平分线AD交BC于点E、交⊙O于点D,延长BD交AC的延长线线于点F,连结CD、OG平分CD.