题目内容
8.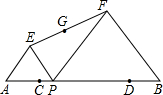 已知线段AB=10,C.D是AB上两点,且AC=DB=2,P是线段CD上一动点,在AB同侧分别作等边三角形APE和等边三角形PBF,G为线段EF的中点,点P由点C移动到点D时,G点移动的路径长度为3.
已知线段AB=10,C.D是AB上两点,且AC=DB=2,P是线段CD上一动点,在AB同侧分别作等边三角形APE和等边三角形PBF,G为线段EF的中点,点P由点C移动到点D时,G点移动的路径长度为3.
分析 分别延长AE、BF交于点M,易证四边形PEMF为平行四边形,得出G为PM中点,则G的运行轨迹△MCD的中位线,运用中位线的性质求出HI的长度即可.
解答 解:如图,分别延长AE、BF交于点M,
∵∠A=∠DPF=60°,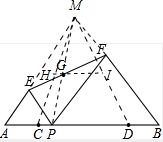
∴AM∥PF,
∵∠B=∠EPA=60°,
∴BM∥PE,
∴四边形PEMF为平行四边形,
∴EF与MP互相平分.
∵G为EF的中点,
∴G正好为PM的中点,
即在P的运动过程中,G始终为PM的中点,
∴G的运行轨迹为△MCD的中位线HI,
∵HI=$\frac{1}{2}$CD=$\frac{1}{2}$×(10-2-2)=3,
∴G点移动的路径长度为3.
故答案为:3.
点评 本题考查了三角形中位线定理及等边三角形的性质,解答本题的关键是作出辅助线,找到点G移动的规律,判断出其运动路径,综合性较强.

练习册系列答案
相关题目
18.下列分解因式正确的是( )
| A. | m2+n2=(m+n)2 | B. | 16m2-4n2=(4m-n)(4m+2n) | ||
| C. | a3-3a2+a=a(a2-3a) | D. | 4a2-4ab+b2=(2a-b)2 |
13.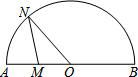 如图,点N是以O为圆心,AB为直径的半圆上的动点,(不与点A,B重合),AB=4,M是OA的中点,设线段MN的长为x,△MNO的面积为y,那么下列图象中,能表示y与x的函数关系的图象大致是( )
如图,点N是以O为圆心,AB为直径的半圆上的动点,(不与点A,B重合),AB=4,M是OA的中点,设线段MN的长为x,△MNO的面积为y,那么下列图象中,能表示y与x的函数关系的图象大致是( )
 如图,点N是以O为圆心,AB为直径的半圆上的动点,(不与点A,B重合),AB=4,M是OA的中点,设线段MN的长为x,△MNO的面积为y,那么下列图象中,能表示y与x的函数关系的图象大致是( )
如图,点N是以O为圆心,AB为直径的半圆上的动点,(不与点A,B重合),AB=4,M是OA的中点,设线段MN的长为x,△MNO的面积为y,那么下列图象中,能表示y与x的函数关系的图象大致是( )| A. | 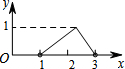 | B. | 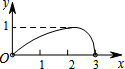 | C. | 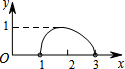 | D. | 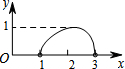 |
20.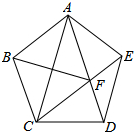 如图,在正五边形ABCDE中,连接AC、AD、CE,CE交AD于点F,连接BF,已知AB=1,则DF的长是( )
如图,在正五边形ABCDE中,连接AC、AD、CE,CE交AD于点F,连接BF,已知AB=1,则DF的长是( )
 如图,在正五边形ABCDE中,连接AC、AD、CE,CE交AD于点F,连接BF,已知AB=1,则DF的长是( )
如图,在正五边形ABCDE中,连接AC、AD、CE,CE交AD于点F,连接BF,已知AB=1,则DF的长是( )| A. | $\frac{\sqrt{5}+1}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | $\frac{\sqrt{5}-1}{2}$ |
18.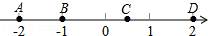 如图,数轴上有A,B,C,D四个点,其中到原点距离相等的两个点是( )
如图,数轴上有A,B,C,D四个点,其中到原点距离相等的两个点是( )
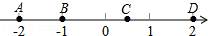 如图,数轴上有A,B,C,D四个点,其中到原点距离相等的两个点是( )
如图,数轴上有A,B,C,D四个点,其中到原点距离相等的两个点是( )| A. | 点B与点D | B. | 点A与点C | C. | 点A与点D | D. | 点B与点C |
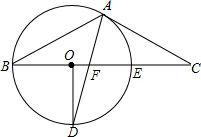 如图,在△ABC中,O是BC上的点,⊙O经过A,B两点,与BC交于点E,D是下半圆的点,且OD⊥BC于点O,并连结AD交BC于点F,若AC是⊙O的切线.
如图,在△ABC中,O是BC上的点,⊙O经过A,B两点,与BC交于点E,D是下半圆的点,且OD⊥BC于点O,并连结AD交BC于点F,若AC是⊙O的切线.