题目内容
5．把一个半径为12，圆心角为150°的扇形围成一个圆锥（接缝处不重叠），那么这个圆锥的高是（ ）| A． | 13 | B． | 5 | C． | $\sqrt{129}$ | D． | $\sqrt{119}$ |
分析 圆锥的底面圆的半径为r，根据圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长和弧长公式得到2πr=$\frac{150•π•12}{180}$，解得r=5，然后根据勾股定理计算圆锥的高．
解答 解：圆锥的底面圆的半径为r，
根据题意得2πr=$\frac{150•π•12}{180}$，解得r=5，
所以圆锥的高=$\sqrt{1{2}^{2}-{5}^{2}}$=$\sqrt{119}$．
故选D．
点评 本题考查了圆锥的计算：圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长．
练习册系列答案
名校课堂系列答案
相关题目
15．
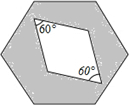如图，边长为a的正六边形，里面有一菱形，边长也为a，空白部分面积为S1，阴影部分面积为S2，则$\frac{{S}_{1}}{{S}_{2}}$=（ ）
如图，边长为a的正六边形，里面有一菱形，边长也为a，空白部分面积为S1，阴影部分面积为S2，则$\frac{{S}_{1}}{{S}_{2}}$=（ ）| A． | $\frac{1}{2}$ | B． | $\frac{1}{3}$ | C． | $\frac{\sqrt{3}}{6}$ | D． | $\frac{\sqrt{3}}{9}$ |
13．
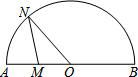如图，点N是以O为圆心，AB为直径的半圆上的动点，（不与点A，B重合），AB=4，M是OA的中点，设线段MN的长为x，△MNO的面积为y，那么下列图象中，能表示y与x的函数关系的图象大致是（ ）
如图，点N是以O为圆心，AB为直径的半圆上的动点，（不与点A，B重合），AB=4，M是OA的中点，设线段MN的长为x，△MNO的面积为y，那么下列图象中，能表示y与x的函数关系的图象大致是（ ）| A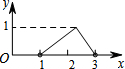． |  | B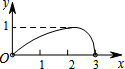． |  | C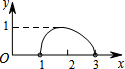． |  | D． |  |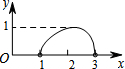
20．
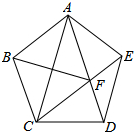如图，在正五边形ABCDE中，连接AC、AD、CE，CE交AD于点F，连接BF，已知AB=1，则DF的长是（ ）
如图，在正五边形ABCDE中，连接AC、AD、CE，CE交AD于点F，连接BF，已知AB=1，则DF的长是（ ）| A． | $\frac{\sqrt{5}+1}{2}$ | B． | $\frac{1}{2}$ | C． | $\frac{\sqrt{5}}{2}$ | D． | $\frac{\sqrt{5}-1}{2}$ |
10．一个三角形的两边长为3和6，第三边的长是方程（x-2）（x-4）=0的根，则这个三角形的周长是（ ）
| A． | 11 | B． | 13 | C． | 11或13 | D． | 11和13 |
14．
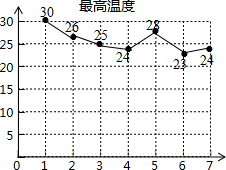五一期间（5月1日-7日），昌平区每天最高温度（单位：℃）情况如图所示，则表示最高温度的这组数据的中位数是（ ）
五一期间（5月1日-7日），昌平区每天最高温度（单位：℃）情况如图所示，则表示最高温度的这组数据的中位数是（ ）| A． | 24 | B． | 25 | C． | 26 | D． | 27 |
如图，四边形ABCD内接于⊙O，∠BCD=100°，AC平分∠BAD，则∠BAC的度数为40°．