题目内容
13. 如图,在平面直角坐标系中,菱形ABCD在第一象限内,边BC与x轴平行,A,B两点的纵坐标分别为3,1.反比例函数y=$\frac{3}{x}$的图象经过A,B两点,则菱形ABCD的面积为( )
如图,在平面直角坐标系中,菱形ABCD在第一象限内,边BC与x轴平行,A,B两点的纵坐标分别为3,1.反比例函数y=$\frac{3}{x}$的图象经过A,B两点,则菱形ABCD的面积为( )| A. | 2 | B. | 4 | C. | 2$\sqrt{2}$ | D. | 4$\sqrt{2}$ |
分析 过点A作x轴的垂线,与CB的延长线交于点E,根据A,B两点的纵坐标分别为3,1,可得出横坐标,即可求得AE,BE,再根据勾股定理得出AB,根据菱形的面积公式:底乘高即可得出答案.
解答  解:过点A作x轴的垂线,与CB的延长线交于点E,
解:过点A作x轴的垂线,与CB的延长线交于点E,
∵A,B两点在反比例函数y=$\frac{3}{x}$的图象上且纵坐标分别为3,1,
∴A,B横坐标分别为1,3,
∴AE=2,BE=2,
∴AB=2$\sqrt{2}$,
S菱形ABCD=底×高=2$\sqrt{2}$×2=4$\sqrt{2}$,
故选D.
点评 本题考查了菱形的性质以及反比例函数图象上点的坐标特征,熟记菱形的面积公式是解题的关键.

练习册系列答案
相关题目
3.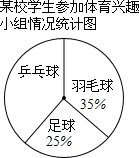 某校学生参加体育兴趣小组情况的统计图如图所示,若参加人数最少的小组有25人,则参加人数最多的小组有( )
某校学生参加体育兴趣小组情况的统计图如图所示,若参加人数最少的小组有25人,则参加人数最多的小组有( )
 某校学生参加体育兴趣小组情况的统计图如图所示,若参加人数最少的小组有25人,则参加人数最多的小组有( )
某校学生参加体育兴趣小组情况的统计图如图所示,若参加人数最少的小组有25人,则参加人数最多的小组有( )| A. | 25人 | B. | 35人 | C. | 40人 | D. | 100人 |
1.已知圆的半径是2$\sqrt{3}$,则该圆的内接正六边形的面积是( )
| A. | 3$\sqrt{3}$ | B. | 9$\sqrt{3}$ | C. | 18$\sqrt{3}$ | D. | 36$\sqrt{3}$ |
8.化简$\sqrt{12}$的结果是( )
| A. | 4$\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 3$\sqrt{2}$ | D. | 2$\sqrt{6}$ |
5.计算(-xy3)2的结果是( )
| A. | x2y6 | B. | -x2y6 | C. | x2y9 | D. | -x2y9 |
 如图,矩形ABCD中,AB=8cm,BC=6cm,动点P从点A出发,以每秒1cm的速度沿线段AB向点B运动,连接DP,把∠A沿DP折叠,使点A落在点A′处.求出当△BPA′为直角三角形时,点P运动的时间.
如图,矩形ABCD中,AB=8cm,BC=6cm,动点P从点A出发,以每秒1cm的速度沿线段AB向点B运动,连接DP,把∠A沿DP折叠,使点A落在点A′处.求出当△BPA′为直角三角形时,点P运动的时间.