题目内容
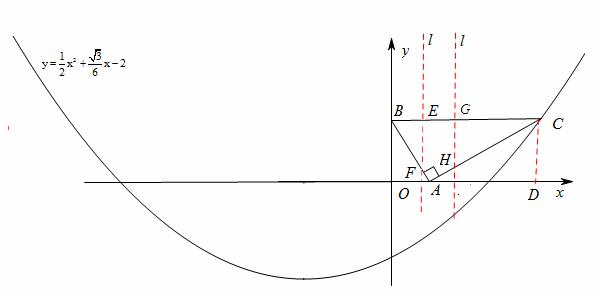
如图,在坐标系xOy中,△ABC中,∠BAC=90°,∠ABC=60°,A(1,0),B(0,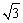 ),抛物线
),抛物线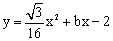 的图象过C点.
的图象过C点.
(1)求抛物线的解析式;
(2)平移该抛物线的对称轴所在直线l.当l移动到何处时,恰好将△ABC的面积分为1 :2的两部分?
:2的两部分?

解:(1)∵A(1,0),B(0,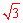 ),
),
∴OA=1,OB=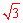 ,AB=2,∠OBA=30°。
,AB=2,∠OBA=30°。
∵△ABC中,∠BAC=90°,∠ABC =60°,
=60°,
∴AC=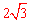 ,BC=4,且BC∥x轴。
,BC=4,且BC∥x轴。
如图所示,过点C作CD⊥x轴于点D,则
∴OD= BC=4,CD=O
BC=4,CD=O B=
B=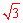 。
。
∴C (4,
(4,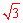 )。
)。
∵点C(4,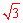 )在抛物线
)在抛物线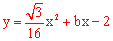 上,
上,
∴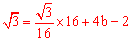 ,解得:
,解得: 。
。
∴抛物线的解析式为: 。
。
(2)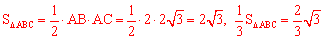 。
。
设直线 AB的解析式为y=kx+b,
AB的解析式为y=kx+b,
∵A(1,0),B(0,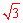 ),
),
∴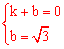 ,解得
,解得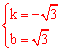 。
。
∴直线AB的解析式为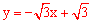 。
。
设直线AC的解析式为y=mx+n,
∵A(1,0),C(4,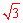 ),
),
∴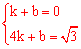 ,解得
,解得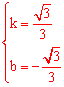 。
。
∴直线AC的解析式为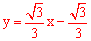 。
。

在△CGH中,由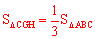 得
得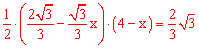 ,即
,即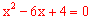
解得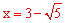
 或
或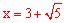 (大于4,不合题意,舍去)。
(大于4,不合题意,舍去)。
∴当直线l解析式为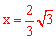 或
或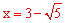 时,恰好将△ABC的面积分为1:2的两
时,恰好将△ABC的面积分为1:2的两 部分。
部分。
【考点】二次函数综合题,动线问题,待定系数法的应用,曲线上点的坐标与方程的关系,含30度直角三角形的性质,分类 思想的应用。
思想的应用。
【分析】(1)根据含30度直角三角形的性质,求出点C的 坐标;然后利用点C的坐标求出抛物线的解析式。
坐标;然后利用点C的坐标求出抛物线的解析式。
(2)分直线l与AB、AC分别相交两种情况讨论即可。

练习册系列答案
相关题目


 B.
B.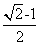
 C.
C.
 D.
D.


 ,点P是以O为圆心,AB为直径的半圆上的动点,AB=2,设弦AP的长为x,△APO的面积为y,则当y=
,点P是以O为圆心,AB为直径的半圆上的动点,AB=2,设弦AP的长为x,△APO的面积为y,则当y= 时,x的取
时,x的取 值是【 】
值是【 】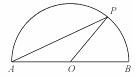
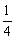 C. 1或
C. 1或 D.
D.  →BC→CD向D点运动,点P的速度是每秒2个单位长度,点Q的速度是每秒1个单位长度,当P运动到D点时,P、Q
→BC→CD向D点运动,点P的速度是每秒2个单位长度,点Q的速度是每秒1个单位长度,当P运动到D点时,P、Q 两点同时停止运动。设P点运动的时间为t,△APQ的面积为S,则S与t的函数关系式是 。
两点同时停止运动。设P点运动的时间为t,△APQ的面积为S,则S与t的函数关系式是 。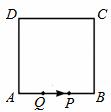
 中,
中,

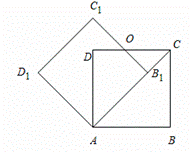
 .将
.将 绕点
绕点 按顺时针方向旋转n度后得到
按顺时针方向旋转n度后得到 ,此时点
,此时点 在
在 边上,斜边
边上,斜边 交
交 边于点
边于点
 ,则n的大小和图中阴影部分的面积分别为【 】
,则n的大小和图中阴影部分的面积分别为【 】
 B.
B. C.
C. D.
D.

 C值最小时PB的长.
C值最小时PB的长.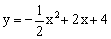 交y轴于点C
交y轴于点C ,对称轴与x轴交于点D,顶点为M,设点P(x,y)是第一象限内该抛物线上的一个动点,直线PE绕点P旋转,
,对称轴与x轴交于点D,顶点为M,设点P(x,y)是第一象限内该抛物线上的一个动点,直线PE绕点P旋转, 与y轴交于点E,是否存在以O、P、E为顶点的三角形与△OPD全等?若存在,请求出点E的坐标;若不存在,请说明理由。
与y轴交于点E,是否存在以O、P、E为顶点的三角形与△OPD全等?若存在,请求出点E的坐标;若不存在,请说明理由。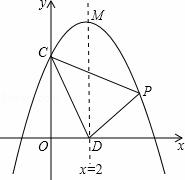
 木棒(AB)长为4,斜靠在与地面(OM)垂直的墙壁(ON)上,与地面的倾斜角(∠ABO)为60°,当木棒A端沿N0向下滑动到A′,B端沿直线OM向右滑动到B′,与地面的倾斜角(∠A′
木棒(AB)长为4,斜靠在与地面(OM)垂直的墙壁(ON)上,与地面的倾斜角(∠ABO)为60°,当木棒A端沿N0向下滑动到A′,B端沿直线OM向右滑动到B′,与地面的倾斜角(∠A′ B′O)为45°,则木棒中点从P随之运动到P′所经
B′O)为45°,则木棒中点从P随之运动到P′所经