题目内容
如图,在平面直角坐标系xOy中,抛物线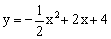 交y轴于点C
交y轴于点C ,对称轴与x轴交于点D,顶点为M,设点P(x,y)是第一象限内该抛物线上的一个动点,直线PE绕点P旋转,
,对称轴与x轴交于点D,顶点为M,设点P(x,y)是第一象限内该抛物线上的一个动点,直线PE绕点P旋转, 与y轴交于点E,是否存在以O、P、E为顶点的三角形与△OPD全等?若存在,请求出点E的坐标;若不存在,请说明理由。
与y轴交于点E,是否存在以O、P、E为顶点的三角形与△OPD全等?若存在,请求出点E的坐标;若不存在,请说明理由。
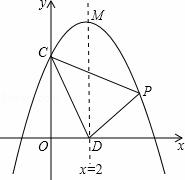
解:∵抛物线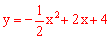 交y轴于点C,
交y轴于点C,
∴C(0,4)。
∵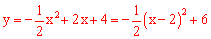 ,
,
∴顶点M坐标为(2,6)。
若以O、P、E为顶点的三角形与△OPD全等,可能有以下情形:
①OD=OP。
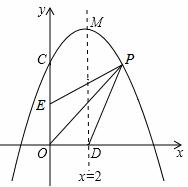
由图象可知,OP最小 值为4,即OP≠OD,故此种情形不存在。
值为4,即OP≠OD,故此种情形不存在。
②OD=OE。

若点P位于第一象限内抛物线对称轴的左侧,易知△OPE为钝角三角形,而△OPD为锐角三角形,则不可能全等。
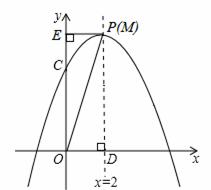
若点P与点M重合,如图2所示,此时△OPD≌OPE,四边形PDOE为矩形。
∴OE=DM=6,即点E的坐标为(0,6)。
综上所述,存在以O、P、E为顶点的三角形与△OPD全等,点E的坐标为(0,2)或(0,6)。
【考点】曲线上点的坐标与方程的关系,二次函数的性质,全等三角形的判定,分类思想和数形结合思想的应用。


练习册系列答案
相关题目
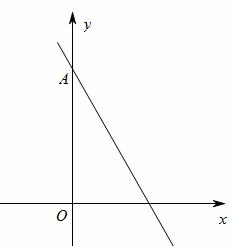
 与
与 轴交于点A,
轴交于点A, 将直线l绕点A顺
将直线l绕点A顺 时针旋转75º后,所得直线的解析式为【 】
时针旋转75º后,所得直线的解析式为【 】
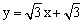 B.
B. C.
C.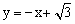 D.
D.
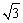 ),抛物线
),抛物线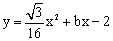 的图象过C点.
的图象过C点. :2的两部分?
:2的两部分?
 的图象经过点A、
的图象经过点A、 B和点C.连接AC,有两动点P、Q同时从点O出发,其中点P以每秒3个单位长度的速度沿折线OAC按O→A→C的路线运动,点Q以每秒8个单位长度的速度沿折线OCA按O→C→A的路线运动,当P、Q两点相遇时,它们都停止运动,设P、Q同时从点O出发t秒时,△OPQ的面
B和点C.连接AC,有两动点P、Q同时从点O出发,其中点P以每秒3个单位长度的速度沿折线OAC按O→A→C的路线运动,点Q以每秒8个单位长度的速度沿折线OCA按O→C→A的路线运动,当P、Q两点相遇时,它们都停止运动,设P、Q同时从点O出发t秒时,△OPQ的面 积为S.
积为S. 并写出自变量t的取值范围;
并写出自变量t的取值范围;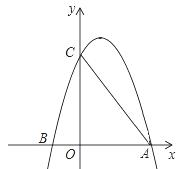



 .
.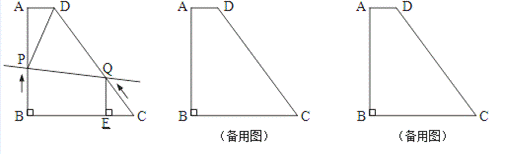

 C→D→A方向向点A运动;过点Q作QE
C→D→A方向向点A运动;过点Q作QE ?若存在,请求出t的值
?若存在,请求出t的值 ,且△ABC≌△DEF,将△DEF与△ABC重合在一起
,且△ABC≌△DEF,将△DEF与△ABC重合在一起 ,△ABC不动,△DEF运动,并满足:点E在边BC上沿B到C的方向运动,且DE始终经过点A,EF与AC交于M点。探究:在△DEF运动过程中,重叠部分能否构成等
,△ABC不动,△DEF运动,并满足:点E在边BC上沿B到C的方向运动,且DE始终经过点A,EF与AC交于M点。探究:在△DEF运动过程中,重叠部分能否构成等
 腰三角形?若
腰三角形?若 能,求出
能,求出 △AEM的面积;若不能,请说明理由。
△AEM的面积;若不能,请说明理由。
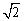 AC。
AC。
 :
: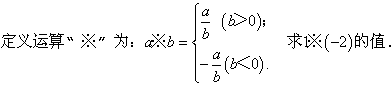

 决问题的:由新定义可知a=1,b=-2,又b<0,所以1※(-2)=
决问题的:由新定义可知a=1,b=-2,又b<0,所以1※(-2)=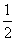
 .
.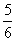
 ,则m= .
,则m= . 函数y=2※x(x≠0)的图象大致是(
函数y=2※x(x≠0)的图象大致是( )
)
