题目内容
7. 如图,是由每个边长都是1的小正方形构成的网格,点O,A,B,M均为格点,P为线段OM上的一个动点.
如图,是由每个边长都是1的小正方形构成的网格,点O,A,B,M均为格点,P为线段OM上的一个动点.(1)点B到OM的距离等于2$\sqrt{2}$;
(2)当点P在线段OM上运动,且使PA2+PB2取得最小值时,请借助网格和无刻度的直尺,在给定的网格中画出点P的位置,并简要说明你是怎么画的.
分析 (1)根据勾股定理即可得到结论;
(2)取格点F,E,连接EF,得到点N,取格点S,T,连接ST,得到点R,连接NR即可得到结果.
解答 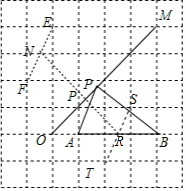 解:(1)点B到OM的距离=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$,
解:(1)点B到OM的距离=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$,
故答案为:2$\sqrt{2}$;(2)以点O为原点建立直角坐标系,则A(1,0),B(4,0),设P(a,a),(0≤a≤4),∵PA2=(a-1)2+a2,PB2=(a-4)2+a2,∴PA2+PB2=4(a-$\frac{5}{4}$)2+$\frac{43}{4}$,
∵0≤a≤4,∴当a=$\frac{5}{4}$时,PA2+PB2 取得最小值 $\frac{43}{4}$,
综上,需作出点P满足线段OP的长=$\frac{5\sqrt{2}}{4}$;
取格点F,E,连接EF,得到点N,取格点S,T,连接ST,得到点R,连接NR交OM于P,
则点P即为所求.
点评 本题考查了作图-应用与设计作图,轴对称-最短距离问题,正确的作出图形是解题的关键.

练习册系列答案
相关题目
18.一元二次方程4x2+1=4x的根的情况是( )
| A. | 只有一个实数根 | B. | 有两个相等的实数根 | ||
| C. | 有两个不相等的实数根 | D. | 没有实数根 |
19.下列命题正确的是( )
| A. | a=$\sqrt{{a}^{2}}$=($\sqrt{a}$)2 | B. | 若$\sqrt{{a}^{2}}$=a,则a=($\sqrt{a}$)2 | C. | (2$\sqrt{-7}$)2=28 | D. | 2$\sqrt{(-4)^{2}}$=-8 |
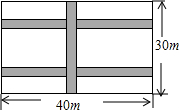 张明的父亲打算在院子里种上蔬菜.已知院子是东西长为40m,南北宽为30m的长方形,为了行走方便,要修筑同样宽的三条道路(如图),东西方向两条,南北方向一条.南北方道路垂直于东西道路,余下的部分分别种上蔬菜.若每条道路的宽为1m,求种蔬菜的土地的总面积.
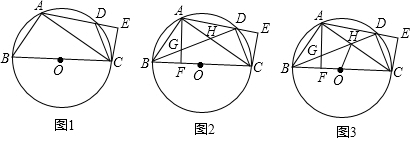
张明的父亲打算在院子里种上蔬菜.已知院子是东西长为40m,南北宽为30m的长方形,为了行走方便,要修筑同样宽的三条道路(如图),东西方向两条,南北方向一条.南北方道路垂直于东西道路,余下的部分分别种上蔬菜.若每条道路的宽为1m,求种蔬菜的土地的总面积.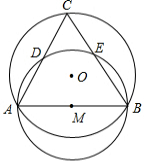 如图,⊙O的半径为2,弦AB的长为2$\sqrt{3}$,以AB为直径作⊙M,点C是优弧$\widehat{AB}$上的一个动点,连接AC、BC,分别交⊙M于点D、E,则线段CD的最大值为2.
如图,⊙O的半径为2,弦AB的长为2$\sqrt{3}$,以AB为直径作⊙M,点C是优弧$\widehat{AB}$上的一个动点,连接AC、BC,分别交⊙M于点D、E,则线段CD的最大值为2.