题目内容
18.一元二次方程4x2+1=4x的根的情况是( )| A. | 只有一个实数根 | B. | 有两个相等的实数根 | ||
| C. | 有两个不相等的实数根 | D. | 没有实数根 |
分析 将方程变形为一般式,根据方程的系数结合根的判别式可得出△=0,由此即可得出结论.
解答 解:原方程可变形为4x2-4x+1=0,
∵在方程4x2-4x+1=0中,△=(-4)2-4×4×1=0,
∴方程4x2+1=4x有两个相等的实数根.
故选B.
点评 本题考查了根的判别式,熟练掌握“当△=0时,方程有两个相等的两个实数根”是解题的关键.

练习册系列答案
相关题目
8.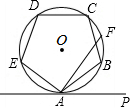 如图,正五边形ABCDE内接于⊙O点F为$\widehat{BC}$的中点,直线AP与⊙O相切于点A,则∠FAP的度数是( )
如图,正五边形ABCDE内接于⊙O点F为$\widehat{BC}$的中点,直线AP与⊙O相切于点A,则∠FAP的度数是( )
 如图,正五边形ABCDE内接于⊙O点F为$\widehat{BC}$的中点,直线AP与⊙O相切于点A,则∠FAP的度数是( )
如图,正五边形ABCDE内接于⊙O点F为$\widehat{BC}$的中点,直线AP与⊙O相切于点A,则∠FAP的度数是( )| A. | 36° | B. | 54° | C. | 60° | D. | 72° |
13.已知三角形的两条边长分别为7和3,则第三边的长不能是( )
| A. | 7 | B. | 6 | C. | 5 | D. | 4 |
10.若|m|=7,n2=81,且m-n>0,则m+n的值为( )
| A. | 2或16 | B. | -2或-16 | C. | ±2 | D. | ±16 |
7. 如图所示,AB∥CD,∠A=∠B,那么下列结论中不成立的是( )
如图所示,AB∥CD,∠A=∠B,那么下列结论中不成立的是( )
 如图所示,AB∥CD,∠A=∠B,那么下列结论中不成立的是( )
如图所示,AB∥CD,∠A=∠B,那么下列结论中不成立的是( )| A. | ∠A=∠3 | B. | ∠B=∠1 | C. | ∠1=∠3 | D. | ∠2+∠B=180° |
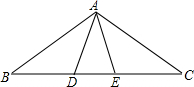 如图,△ABC中,AB=AC,∠B=∠C,点D,E在BC边上,添加一个适当的条件BE=CD时,可以使△ABE≌△ACD.
如图,△ABC中,AB=AC,∠B=∠C,点D,E在BC边上,添加一个适当的条件BE=CD时,可以使△ABE≌△ACD. 如图,是由每个边长都是1的小正方形构成的网格,点O,A,B,M均为格点,P为线段OM上的一个动点.
如图,是由每个边长都是1的小正方形构成的网格,点O,A,B,M均为格点,P为线段OM上的一个动点.