题目内容
5. 如图,菱形ABCD中,AB=5,BD=6,则菱形的高为( )
如图,菱形ABCD中,AB=5,BD=6,则菱形的高为( )| A. | $\frac{12}{5}$ | B. | $\frac{24}{5}$ | C. | 12 | D. | 24 |
分析 直接利用菱形的性质得出AC的长,进而利用菱形的面积求出答案.
解答  解:∵菱形ABCD中,BD=6,
解:∵菱形ABCD中,BD=6,
∴BO=3,∠AOB=90°,
∴AO=CO=$\sqrt{A{B}^{2}-B{O}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4,
∴AC=8,
∴设菱形的高为x,则5x=$\frac{1}{2}$×6×8,
解得:x=$\frac{24}{5}$.
故选:B.
点评 此题主要考查了菱形的性质以及勾股定理,正确得出AC的长是解题关键.

练习册系列答案
相关题目
15.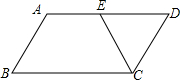 如图,在平行四边形ABCD中,AD=2AB,CE平分∠BCD交AD边 于点E,且AE=3,则AB的长为( )
如图,在平行四边形ABCD中,AD=2AB,CE平分∠BCD交AD边 于点E,且AE=3,则AB的长为( )
 如图,在平行四边形ABCD中,AD=2AB,CE平分∠BCD交AD边 于点E,且AE=3,则AB的长为( )
如图,在平行四边形ABCD中,AD=2AB,CE平分∠BCD交AD边 于点E,且AE=3,则AB的长为( )| A. | 4 | B. | 3 | C. | $\frac{5}{2}$ | D. | 2 |
20.下列命题中,真命题是( )
| A. | 连接矩形各边中点的四边形是菱形 | B. | 对角线垂直的四边形是菱形 | ||
| C. | 三个角相等的四边形是矩形 | D. | 两条对角线相等的四边形是矩形 |

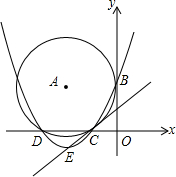 如图,在平面直角坐标系中,⊙A与x轴相交于C(-2,0),D(-8,0)两点,与y轴相切于点B(0,4).
如图,在平面直角坐标系中,⊙A与x轴相交于C(-2,0),D(-8,0)两点,与y轴相切于点B(0,4).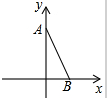 如图,在平面直角坐标系中,点A,B的坐标分别为(0,1)和$(\sqrt{3},0)$,若在第四象限存在点C,使△OBC和△OAB相似,则点C的坐标是($\sqrt{3}$,-1),或($\sqrt{3}$,3)或($\frac{\sqrt{3}}{4}$,-$\frac{3}{4}$)或($\frac{3\sqrt{3}}{4}$,-$\frac{3}{4}$).
如图,在平面直角坐标系中,点A,B的坐标分别为(0,1)和$(\sqrt{3},0)$,若在第四象限存在点C,使△OBC和△OAB相似,则点C的坐标是($\sqrt{3}$,-1),或($\sqrt{3}$,3)或($\frac{\sqrt{3}}{4}$,-$\frac{3}{4}$)或($\frac{3\sqrt{3}}{4}$,-$\frac{3}{4}$).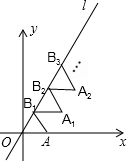 如图放置的△OAB1,△B1A1B2,△B2A2B3,…都是边长为1的等边三角形,点A在x轴上,点O,B1,B2,B3,…都在正比例函数y=kx的图象l上,则点B2014的坐标是(1007,1007$\sqrt{3}$).
如图放置的△OAB1,△B1A1B2,△B2A2B3,…都是边长为1的等边三角形,点A在x轴上,点O,B1,B2,B3,…都在正比例函数y=kx的图象l上,则点B2014的坐标是(1007,1007$\sqrt{3}$).