题目内容
已知函数y=-2x+4.
(1)当x>-2时,求函数值y的取值范围;
(2)当y<-2时,求自变量x的取值范围.
(1)当x>-2时,求函数值y的取值范围;
(2)当y<-2时,求自变量x的取值范围.
考点:一次函数与一元一次不等式
专题:
分析:(1)先用y的代数式表示x,即x=
,然后由x>-2,得到
>-2,解不等式,即可得出函数值y的取值范围;
(2)由y<-2得到-2x+4<-2,解不等式,即可得出自变量x的取值范围.
| 4-y |
| 2 |
| 4-y |
| 2 |
(2)由y<-2得到-2x+4<-2,解不等式,即可得出自变量x的取值范围.
解答:解:(1)∵y=-2x+4,
∴x=
,
∵x>-2,
∴
>-2,
解不等式,得y<8;
(2)∵y=-2x+4,y<-2,
∴-2x+4<-2,
解不等式,x>3.
∴x=
| 4-y |
| 2 |
∵x>-2,
∴
| 4-y |
| 2 |
解不等式,得y<8;
(2)∵y=-2x+4,y<-2,
∴-2x+4<-2,
解不等式,x>3.
点评:此题主要考查了一次函数的图象性质,同时考查了解不等式的方法,同学们要熟练掌握.

练习册系列答案
相关题目
在平面内,⊙O的半径为2cm,圆心O到直线l的距离为3cm,则直线l与⊙O的位置关系是( )
| A、内含 | B、相交 | C、相切 | D、相离 |
 如图,在平面直角坐标系中,O为原点,点A、B的坐标分别为(4,0),(2,-6),将△OAB绕AB的中点旋转180°,点O落到点C的位置,抛物线经过点O、A、C,点D是该抛物线的顶点.
如图,在平面直角坐标系中,O为原点,点A、B的坐标分别为(4,0),(2,-6),将△OAB绕AB的中点旋转180°,点O落到点C的位置,抛物线经过点O、A、C,点D是该抛物线的顶点.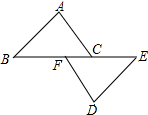 如图,点B、F、C、E在同一条直线上,FB=CE,AB∥ED,AC∥FD.
如图,点B、F、C、E在同一条直线上,FB=CE,AB∥ED,AC∥FD.