题目内容
8．
如图所示：∠CAB=∠BCD，AD=2，BD=4，则BC=（ ）| A． | $2\sqrt{2}$ | B． | $2\sqrt{6}$ | C． | 3 | D． | 6 |
分析 两角对应相等的两个三角形相似可证得△ABC∽△CBD，再根据相似三角形的性质可解．
解答 解：∵∠B=∠B，∠CAB=∠BCD
∴△ABC∽△CBD
∴BC：BD=AB：BC
∴BC：BD=（AD+BD）：BC
即BC：4=（2+4）：BC
∴BC=2$\sqrt{6}$，
故选B
点评 此题考查相似三角形的判定定理及性质，关键是根据两角对应相等的两个三角形相似可证得△ABC∽△CBD．
练习册系列答案
相关题目
9．下列方程中，是一元一次方程的是（ ）
| A． | x+y=2 | B． | x2-x-2=0 | C． | $\frac{3}{x}$+1=$\frac{1}{2}$ | D． | $\frac{1}{3}$x-$\frac{1}{2}$=$\frac{3}{2}$x |
16．
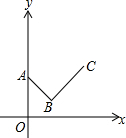如图，某个函数的图象由线段AB和BC组成，其中点A（0，1.1），B（1，0.5），C（2，1.3），则此函数的最小值是（ ）
如图，某个函数的图象由线段AB和BC组成，其中点A（0，1.1），B（1，0.5），C（2，1.3），则此函数的最小值是（ ）| A． | 0 | B． | 1.1 | C． | 0.5 | D． | 1.3 |
3．若函数y=$\frac{1}{2}$（x2-100x+196+|x2-100x+196|），则自变量x取1，2，3，4，…99，100这100个自然数时，函数和的值是（ ）
| A． | 540 | B． | 390 | C． | 194 | D． | 97 |
等腰直角三角形ABC，∠ABC=90°，AB=2，O为AC中点，∠EOF=45°，求△BEF的周长．
20．一根绳子对折3次，每段长是全长的（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{1}{4}$ | C． | $\frac{1}{6}$ | D． | $\frac{1}{8}$ |
