题目内容
7.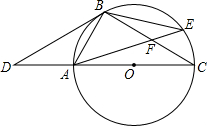 如图,点D是⊙O的直径CA延长线上的一点,点B在⊙O上,且AB=AD=AO.
如图,点D是⊙O的直径CA延长线上的一点,点B在⊙O上,且AB=AD=AO.(1)求证:BD是⊙O的切线;
(2)若点E是劣弧BC上一点,AE与BC相交于点F,且∠ABE=105°,S△BEF=8($\sqrt{3}$-1),求△ACF的面积和CF的长.
分析 (1)根据已知条件证得△ABO为等边三角形,根据三角形外角的性质可求得∠ABD=∠ADB=30°,则可求得∠OBD=90°,BD是⊙O的切线;
(2)先求得∠CAF=∠EBF=15°,进而求得∠BAF=45°,可求得sin45°=$\frac{BF}{AF}$=$\frac{\sqrt{2}}{2}$,根据同弧所对的圆周角相等,可证明△ACF∽△BEF,得出一相似比,再利用三角形的面积比等于相似比的平方即可求得△ACF的面积,通过解直角三角形ABC和等腰三角形的性质得出BC=$\sqrt{3}$BF,得出FC=($\sqrt{3}$-1)BF,然后根据S△ACF=$\frac{1}{2}$CF•AB=$\frac{1}{2}$CF•BF=16($\sqrt{3}$-1),即可求得CF的长.
解答 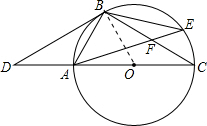 (1)证明:连接BO,
(1)证明:连接BO,
∵AB=AO,BO=AO,
∴AB=AO=BO,
∴△ABO为等边三角形,
∴∠BAO=∠ABO=60°,
∵AB=AD,
∴∠D=∠ABD,
又∵∠D+∠ABD=∠BAO=60°,
∴∠ABD=30°,
∴∠OBD=∠ABD+∠ABO=90°,即BD⊥BO,
∴BD是⊙O的切线;
(2)解:∵∠ABC=90°,∠ABE=105°,
∴∠CAF=∠EBF=15°,
∵∠BAO=60°,
∴∠BAF=45°,
∴sin45°=$\frac{BF}{AF}$=$\frac{\sqrt{2}}{2}$,
∵∠C=∠E,∠CAF=∠EBF,
∴△ACF∽△BEF,
∴$\frac{{S}_{△BEF}}{{S}_{△ACF}}$=( $\frac{BF}{AF}$)2=$\frac{1}{2}$,
又∵S△BEF=8($\sqrt{3}$-1),
∴S△ACF=16($\sqrt{3}$-1).
在RT△ABC中,
∵∠BAC=60°,
∴BC=$\sqrt{3}$AB,
∵AB=BF,
∴BC=$\sqrt{3}$BF,
∴FC=($\sqrt{3}$-1)BF,
∴S△ACF=$\frac{1}{2}$CF•AB=$\frac{1}{2}$CF•BF=16($\sqrt{3}$-1),
∴$\frac{1}{2}$CF•BF=$\frac{1}{2}$($\sqrt{3}$-1)BF•BF=16($\sqrt{3}$-1),
∴BF=4$\sqrt{2}$,
∴CF=($\sqrt{3}$-1)×$4\sqrt{2}$=4$\sqrt{6}$-4$\sqrt{2}$.
点评 本题综合考查了圆的切线的性质、圆的性质、相似三角形的判定及性质等内容,是一个综合较强的题目,难度较大.

| 克服酒驾--你认为哪种方式最好?(单选) |
| A、加强宣传,增强意识. B、在汽车上张贴“请勿酒驾”字样. C、司机上岗前签“拒接酒驾”保证书. D、加大检查力度,严惩酒驾行为. E、查出酒驾追究整个家庭责任. |
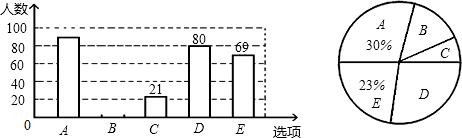
根据上述信息,解答下列问题:
(1)本次抽样调查的样本容量是多少?
(2)补全条形图,并计算B选项所对应扇形圆心角的度数;
(3)若该市有30000名司机,估计支持D选项的司机大约有多少人?
| A. | 打开电视,正在播放广告 | B. | 三角形三个内角的和是180° | ||
| C. | 两个负数的和是正数 | D. | 某名牌产品一定是合格产品 |
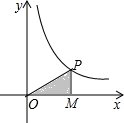 如图,点P为反比例函数y=$\frac{16}{x}$在第一象限图象上的动点,过点P作x轴的垂线,垂足为M,则三角形OPM的面积为8.
如图,点P为反比例函数y=$\frac{16}{x}$在第一象限图象上的动点,过点P作x轴的垂线,垂足为M,则三角形OPM的面积为8.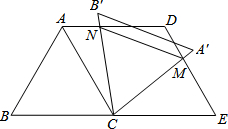 如图,已知等边△ABC的边长是2cm,将边AC沿射线BC的方向平移2cm,得到线段DE,连接AD、CE.
如图,已知等边△ABC的边长是2cm,将边AC沿射线BC的方向平移2cm,得到线段DE,连接AD、CE.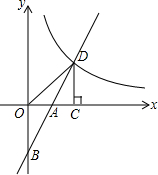 如图,在平面直角坐标系中,直线y=2x+b(b<0)与坐标轴交于A,B两点,与双曲线y=$\frac{k}{x}$(x>0)交于D点,过点D作DC⊥x轴于点C,连接OD.已知△AOB≌△ACD.
如图,在平面直角坐标系中,直线y=2x+b(b<0)与坐标轴交于A,B两点,与双曲线y=$\frac{k}{x}$(x>0)交于D点,过点D作DC⊥x轴于点C,连接OD.已知△AOB≌△ACD.