题目内容
在一个不不透明的口袋中装有5个白球，若干个黑球，它们除颜色外其他完全相同，经过多次实验发现摸到白球的频率稳定在0.2附近，则黑球大约有 个．
考点：利用频率估计概率
专题：
分析：由摸到白球的频率稳定在0.2附近得出口袋中得到白色球的概率，进而求出黑球个数即可．
解答：解：设黑球个数为：x个，
∵摸到白色球的频率稳定在0.2左右，
∴口袋中得到白色球的概率为0.2，
∴
=
，
解得：x=20，
故黑球的个数为20个．
故答案为：20．
∵摸到白色球的频率稳定在0.2左右，
∴口袋中得到白色球的概率为0.2，
∴
| 5 |
| 5+x |
| 1 |
| 5 |
解得：x=20，
故黑球的个数为20个．
故答案为：20．
点评：此题主要考查了利用频率估计概率，根据大量反复试验下频率稳定值即概率得出是解题关键．
练习册系列答案
相关题目
抛物线y=x2-kx-3与x轴交于点A，B，与y轴交于点C，其中点B的坐标为（1+k，0）．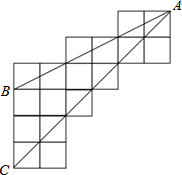
如图，△ABC的三个点顶均在正方形网格格点上，求tan∠BAC=
如图，双曲线y=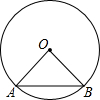
如图，⊙O的半径OA，OB，且OA⊥OB，连结AB．在⊙O上找一点C，使OA2+AB2=BC2，则∠OAC的度数为下列说法中正确的是（ ）
| A、-4没有立方根 | ||||
| B、1的立方根是±1 | ||||
C、
| ||||
D、-5的立方根是
|