题目内容
 如图,双曲线y=
如图,双曲线y=| k1 |
| x |
| k2 |
| x |
| k1 |
| x |
| k2 |
| x |
考点:反比例函数系数k的几何意义
专题:
分析:设A(a,b),B(c,d),代入双曲线得到K1=ab,K2=cd,根据三角形的面积公式求出cd-ab=24,即可得出答案.
解答:解:设A(a,b),B(c,d),
代入得:K1=ab,K2=cd,
∵S△AOB=12,
∴
ab-
cd=12,
∴ab-cd=24,
∴K2-K1=-24,
故答案为-24.
代入得:K1=ab,K2=cd,
∵S△AOB=12,
∴
| 1 |
| 2 |
| 1 |
| 2 |
∴ab-cd=24,
∴K2-K1=-24,
故答案为-24.
点评:本题主要考查对反比例函数系数的几何意义,反比例函数图象上点的坐标特征,三角形的面积等知识点的理解和掌握,能求出cd-ab=4是解此题的关键.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
-|-3|的值为( )
| A、-3 | ||
| B、3 | ||
C、
| ||
D、-
|
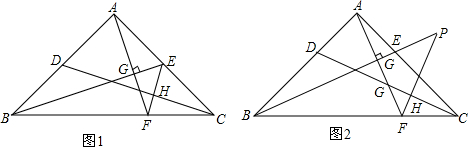
 如图,在△ABC中,AB=AC=13,DE是△ABC的中位线,F是DE的中点.已知B(-1,0),C(9,0),则点F的坐标为
如图,在△ABC中,AB=AC=13,DE是△ABC的中位线,F是DE的中点.已知B(-1,0),C(9,0),则点F的坐标为 如图,直线y=3x+3与x轴交于点A,与y轴交于点B.过B点作直线BP与x轴正半轴交于点P,取线段OA、OB、OP,当其中一条线段的长是其他两条线段长度的比例中项时,则P点的坐标为
如图,直线y=3x+3与x轴交于点A,与y轴交于点B.过B点作直线BP与x轴正半轴交于点P,取线段OA、OB、OP,当其中一条线段的长是其他两条线段长度的比例中项时,则P点的坐标为