题目内容
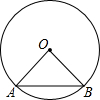 如图,⊙O的半径OA,OB,且OA⊥OB,连结AB.在⊙O上找一点C,使OA2+AB2=BC2,则∠OAC的度数为
如图,⊙O的半径OA,OB,且OA⊥OB,连结AB.在⊙O上找一点C,使OA2+AB2=BC2,则∠OAC的度数为考点:垂径定理,解直角三角形
专题:分类讨论
分析:设圆的半径是r,作直径BD,作BC关于直径BD的对称线段BE,连接EC,BE,ED,AC,再由直角三角形的性质即可解答.
解答: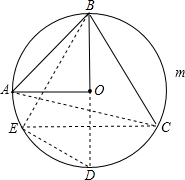 解:如图,设圆的半径是r,则AO=r,BO=r,作直径BD,作BC⊙O的弦BC,使∠DBC=30°,作BC关于直径BD的对称线段BE,
解:如图,设圆的半径是r,则AO=r,BO=r,作直径BD,作BC⊙O的弦BC,使∠DBC=30°,作BC关于直径BD的对称线段BE,
连接EC,BE,ED,AC,
直角△BED中,可以得∠EBD=30°,
∵线段BE与线段BC关于直线BD对称,
∴BC=BE,
∴BD垂直平分线段CE,
∴
=
,
∴∠CBD=30°而∠BCA=
∠AOB=45°.
在△ABC中,∠OAC=180°-∠ABO-∠CBD-∠ACB-∠BAO=15°.
同理,当E为C时,∠OAC=75°.
可得,∠OAC的度数为15°或75°.
故答案为:15°或75°.
 解:如图,设圆的半径是r,则AO=r,BO=r,作直径BD,作BC⊙O的弦BC,使∠DBC=30°,作BC关于直径BD的对称线段BE,
解:如图,设圆的半径是r,则AO=r,BO=r,作直径BD,作BC⊙O的弦BC,使∠DBC=30°,作BC关于直径BD的对称线段BE,连接EC,BE,ED,AC,
直角△BED中,可以得∠EBD=30°,
∵线段BE与线段BC关于直线BD对称,
∴BC=BE,
∴BD垂直平分线段CE,
∴
 |
| DE |
 |
| CD |
∴∠CBD=30°而∠BCA=
| 1 |
| 2 |
在△ABC中,∠OAC=180°-∠ABO-∠CBD-∠ACB-∠BAO=15°.
同理,当E为C时,∠OAC=75°.
可得,∠OAC的度数为15°或75°.
故答案为:15°或75°.
点评:本题考查的是圆心角、弧、弦的关系及直角三角形的性质,根据题意作出辅助线是解答此题的关键.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
 如图,直线y=3x+3与x轴交于点A,与y轴交于点B.过B点作直线BP与x轴正半轴交于点P,取线段OA、OB、OP,当其中一条线段的长是其他两条线段长度的比例中项时,则P点的坐标为
如图,直线y=3x+3与x轴交于点A,与y轴交于点B.过B点作直线BP与x轴正半轴交于点P,取线段OA、OB、OP,当其中一条线段的长是其他两条线段长度的比例中项时,则P点的坐标为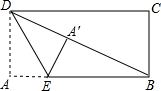 如图,在矩形纸片ABCD中,AB=12,BC=5,点E在AB上,将△DAE沿DE折叠,使点A落在对角线BD上的点A′处,则AE的长为( )
如图,在矩形纸片ABCD中,AB=12,BC=5,点E在AB上,将△DAE沿DE折叠,使点A落在对角线BD上的点A′处,则AE的长为( )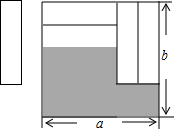 如图,把四张形状大小完全相同的小长方形卡片不重叠地放在一个底面为长方形(长为a,宽为b)的盒子底部,盒子底面未被卡片覆盖的部分用阴影表示,则这两块阴影部分小长方形周长的和为( )
如图,把四张形状大小完全相同的小长方形卡片不重叠地放在一个底面为长方形(长为a,宽为b)的盒子底部,盒子底面未被卡片覆盖的部分用阴影表示,则这两块阴影部分小长方形周长的和为( )