题目内容
1．?ABCD中，∠A：∠B：∠C：∠D的值可以等于（ ）| A． | 1：2：3：4 | B． | 3：4：4：3 | C． | 3：3：4：4 | D． | 3：4：3：4 |
分析 根据平行四边形的性质得到∠A=∠C，∠B=∠D，∠B+∠C=180°，∠A+∠D=180°，根据以上结论即可选出答案即可．
解答 解：∵四边形ABCD是平行四边形，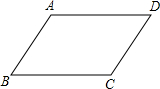
∴∠A=∠C，∠B=∠D，AB∥CD，
∴∠B+∠C=180°，∠A+∠D=180°，
即∠A和∠C的数相等，∠B和∠D的数相等，且∠B+∠C=∠A+∠D．
故选D．
点评 本题主要考查了平行四边形的性质，能根据平行四边形的对角相等及平行线的性质进行判断是解此题的关键．
练习册系列答案
精英口算卡系列答案
应用题点拨系列答案
状元及第系列答案
相关题目
9．
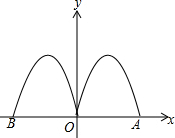如图，抛物线y=-2x2+4x与x轴交于点O、A，把抛物线在x轴及其上方的部分记为C1，将C1以y铀为对称轴作轴对称得到C2，C2与x轴交于点B，若直线y=x+m与C1，C2共有3个不同的交点，则m的取值范围是（ ）
如图，抛物线y=-2x2+4x与x轴交于点O、A，把抛物线在x轴及其上方的部分记为C1，将C1以y铀为对称轴作轴对称得到C2，C2与x轴交于点B，若直线y=x+m与C1，C2共有3个不同的交点，则m的取值范围是（ ）| A． | 0＜m$＜\frac{9}{8}$ | B． | $\frac{9}{8}$＜m＜$\frac{25}{8}$ | C． | 0＜m＜$\frac{25}{8}$ | D． | m＜$\frac{9}{8}$或m＜$\frac{25}{8}$ |
16．
如图，直线AB∥CD，BC平分∠ABD，∠1=65°，则∠2的度数为（ ）
如图，直线AB∥CD，BC平分∠ABD，∠1=65°，则∠2的度数为（ ）| A． | 65° | B． | 50° | C． | 45° | D． | 40° |
6．不等式的-x＜2解集在数轴上表示如下，正确的是（ ）
| A． |  | B． |  | ||
| C． |  | D． |  |
13．如果一个多边形的内角和是1800°，这个多边形是（ ）
| A． | 八边形 | B． | 十四边形 | C． | 十边形 | D． | 十二边形 |
10．下列成语所描述的事件是必然事件的是（ ）
| A． | 瓮中捉鳖 | B． | 守株待兔 | C． | 拔苗助长 | D． | 水中捞月 |