题目内容
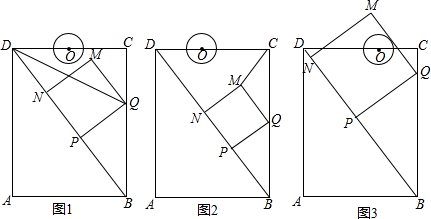
14.如图,在矩形ABCD中,AB=6cm,AD=8cm,点P从点B出发,沿对角线BD向点D匀速运动,速度为4cm/s,过点P作PQ⊥BD交BC于点Q,以PQ为一边作正方形PQMN,使得点N落在射线PD上,点O从点D出发,沿DC向点C匀速运动,速度为3m/s,以O为圆心,0.8cm为半径作⊙O,点P与点O同时出发,设它们的运动时间为t(单位:s)(0<t<$\frac{8}{5}$).(1)如图1,连接DQ平分∠BDC时,t的值为1;
(2)如图2,连接CM,若△CMQ是以CQ为底的等腰三角形,求t的值;
(3)请你继续进行探究,并解答下列问题:
①证明:在运动过程中,点O始终在QM所在直线的左侧;
②如图3,在运动过程中,当QM与⊙O相切时,求t的值;并判断此时PM与⊙O是否也相切?说明理由.
分析 (1)先利用△PBQ∽△CBD求出PQ、BQ,再根据角平分线性质,列出方程解决问题.
(2)由△QTM∽△BCD,得$\frac{QM}{BD}$=$\frac{TQ}{BC}$列出方程即可解决.
(3)①如图2中,延长QM交CD于E,求出DE、DO利用差值比较即可解决问题.
②如图3中,由①可知⊙O只有在左侧与直线QM相切于点H,QM与CD交于点E.由△OHE∽△BCD,得$\frac{OH}{BC}$=$\frac{OE}{BD}$,列出方程即可解决问题.利用反证法证明直线PM不可能由⊙O相切.
解答 (1)解:如图1中, ∵四边形ABCD是矩形,
∵四边形ABCD是矩形,
∴∠A=∠C=∠ADC=∠ABC=90°,AB=CD=6.AD=BC=8,
∴BD=$\sqrt{A{D}^{2}+A{B}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}$=10,
∵PQ⊥BD,
∴∠BPQ=90°=∠C,
∵∠PBQ=∠DBC,
∴△PBQ∽△CBD,
∴$\frac{PB}{BC}$=$\frac{PQ}{DC}$=$\frac{BQ}{BD}$,
∴$\frac{4t}{8}$=$\frac{PQ}{6}$=$\frac{BQ}{10}$,
∴PQ=3t,BQ=5t,
∵DQ平分∠BDC,QP⊥DB,QC⊥DC,
∴QP=QC,
∴3t=8-5t,
∴t=1,
故答案为:1.
(补充:直接利用角平分线的性质得到DP=DC=6,BP=4,从而t=1)
(2)解:如图2中, 作MT⊥BC于T.
作MT⊥BC于T.
∵MC=MQ,MT⊥CQ,
∴TC=TQ,
由(1)可知TQ=$\frac{1}{2}$(8-5t),QM=3t,
∵MQ∥BD,
∴∠MQT=∠DBC,
∵∠MTQ=∠BCD=90°,
∴△QTM∽△BCD,
∴$\frac{QM}{BD}$=$\frac{TQ}{BC}$,
∴$\frac{3t}{10}$=$\frac{\frac{1}{2}(8-5t)}{8}$,
∴t=$\frac{40}{49}$(s),
∴t=$\frac{40}{49}$s时,△CMQ是以CQ为底的等腰三角形.
(3)①证明:如图2中,延长QM交CD于E,
∵EQ∥BD,
∴$\frac{EC}{CD}$=$\frac{CQ}{CB}$,
∴EC=$\frac{3}{4}$(8-5t),ED=DC-EC=6-$\frac{3}{4}$(8-5t)=$\frac{15}{4}$t,
∵DO=3t,
∴DE-DO=$\frac{15}{4}$t-3t=$\frac{3}{4}$t>0,
∴点O在直线QM左侧.
②解:如图3中,由①可知⊙O只有在左侧与直线QM相切于点H,QM与CD交于点E.
∵EC=$\frac{3}{4}$(8-5t),DO=3t,
∴OE=6-3t-$\frac{3}{4}$(8-5t)=$\frac{3}{4}$t,
∵OH⊥MQ,
∴∠OHE=90°,
∵∠HEO=∠CEQ,
∴∠HOE=∠CQE=∠CBD,
∵∠OHE=∠C=90°,
∴△OHE∽△BCD,
∴$\frac{OH}{BC}$=$\frac{OE}{BD}$,
∴$\frac{\frac{4}{5}}{8}$=$\frac{\frac{3}{4}t}{10}$,
∴t=$\frac{4}{3}$.
∴t=$\frac{4}{3}$s时,⊙O与直线QM相切.
连接PM,假设PM与⊙O相切,则∠OMH=$\frac{1}{2}$PMQ=22.5°,
在MH上取一点F,使得MF=FO,则∠FMO=∠FOM=22.5°,
∴∠OFH=∠FOH=45°,
∴OH=FH=$\frac{4}{5}$,FO=FM=$\frac{4}{5}$$\sqrt{2}$,
∴MH=$\frac{4}{5}$($\sqrt{2}$+1),
由$\frac{OH}{BC}$=$\frac{HE}{DC}$得到HE=$\frac{3}{5}$,
由$\frac{EC}{BD}$=$\frac{CQ}{CB}$得到EQ=$\frac{5}{3}$,
∴MH=MQ-HE-EQ=4-$\frac{3}{5}$-$\frac{5}{3}$=$\frac{26}{15}$,
∴$\frac{4}{5}$($\sqrt{2}$+1)≠$\frac{26}{15}$,矛盾,
∴假设不成立.
∴直线PM与⊙O不相切.
点评 本题考查圆综合题、正方形的性质、相似三角形的判定和性质、切线的判定和性质、勾股定理、角平分线的性质等知识,解题的关键灵活运用这些知识解决问题,学会利用方程的思想思考问题,充分利用相似三角形的性质构建方程,在最后一个问题证明中利用了反证法,属于中考压轴题.

| A. | -15 | B. | -16 | C. | 15 | D. | 16 |
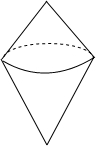 如图所示的几何体左视图是( )
如图所示的几何体左视图是( )| A. | 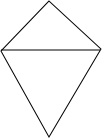 | B. | 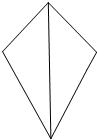 | C. | 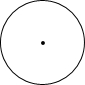 | D. | 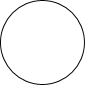 |
| A. | cos40°=sin50° | B. | tan15°•tan75°=1 | ||
| C. | sin225°+cos225°=1 | D. | sin60°=2sin30° |
| A. | 3,4,4 | B. | 3,4,5 | C. | 3,4,6 | D. | 3,4,7 |
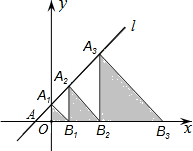 如图,在平面直角坐标系中,直线l:y=x+2交x轴于点A,交y轴于点A1,点A2,A3,…在直线l上,点B1,B2,B3,…在x轴的正半轴上,若△A1OB1,△A2B1B2,△A3B2B3,…,依次均为等腰直角三角形,直角顶点都在x轴上,则第n个等腰直角三角形AnBn-1Bn顶点Bn的横坐标为2n+1-2.
如图,在平面直角坐标系中,直线l:y=x+2交x轴于点A,交y轴于点A1,点A2,A3,…在直线l上,点B1,B2,B3,…在x轴的正半轴上,若△A1OB1,△A2B1B2,△A3B2B3,…,依次均为等腰直角三角形,直角顶点都在x轴上,则第n个等腰直角三角形AnBn-1Bn顶点Bn的横坐标为2n+1-2.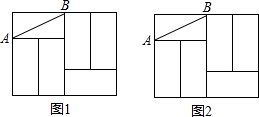 如图,六个完全相同的小长方形拼成了一个大长方形,AB是其中一个小长方形的对角线,请在大长方形中完成下列画图,要求:①仅用无刻度直尺,②保留必要的画图痕迹.
如图,六个完全相同的小长方形拼成了一个大长方形,AB是其中一个小长方形的对角线,请在大长方形中完成下列画图,要求:①仅用无刻度直尺,②保留必要的画图痕迹. 在平面直角坐标系中,△ABC三个顶点坐标为A(-$\sqrt{3}$,0)、B($\sqrt{3}$,0)、C(0,3).
在平面直角坐标系中,△ABC三个顶点坐标为A(-$\sqrt{3}$,0)、B($\sqrt{3}$,0)、C(0,3).