题目内容
13．
如图，OE是△ABC的边AC的垂直平分线，AO平分∠BAC，EO交AB的延长线于点D，连接CD，求证：CO平分∠ACD．
分析 根据线段的垂直平分线的性质得到OA=OC，DA=DC．根据等腰三角形的性质、角平分线的定义证明即可．
解答 证明：∵OE是△ABC的边AC的垂直平分线，
∴OA=OC，DA=DC，
∴∠OCA=∠OAC，∠DCA=∠DAC，
∴∠DCO=∠DAO，
∵AO平分∠BAC，
∴CO平分∠ACD．
点评 本题考查的是线段的垂直平分线的性质，掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
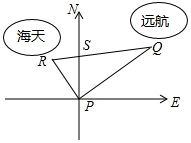某港口位于东西方向的海岸线上，“远航”号、“海天”号轮船同时离开港口，各自沿一固定的方向航行，“远航”号每小时航行16海里，“海天”号每小时航行12海里．它们离开港口$\frac{1}{2}$小时后相距10海里．如果知道“远航”号沿东北方向航行，能知道“海天”号沿哪个方向航行吗？
4．已知|2x+3|=-2x-3，则x的取值范围是（ ）
| A． | x＞-$\frac{3}{2}$ | B． | x＜-$\frac{3}{2}$ | C． | x≥-$\frac{3}{2}$ | D． | x≤-$\frac{3}{2}$ |
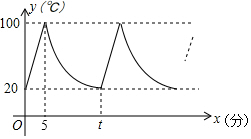如图所示，小明家饮水机中原有水的温度是20℃，开机通电后，饮水机自动开始加热，此过程中水温y（℃）与开机时间x（分）满足一次函数关系．当加热到100℃时自动停止加热，随后水温开始下降，此过程中水温y（℃）与开机时间x（分）成反比例关系．当水温降至20℃时，饮水机又自动开始加热…，不断重复上述程序．根据图中提供的信息，解答下列问题：
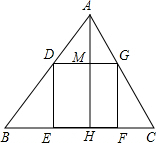如图，正方形DEFG的边EF在△ABC的边BC上，顶点D、G分别在边AB、AC上，已知△ABC的边BC=15，高AH=10，求正方形DEFG的边长和面积．
5．直线 y=x-1与坐标轴交于A、B两点，点C在x轴上，若△ABC为等腰三角形且S△ABC=$\frac{\sqrt{2}}{2}$，则点C的坐标为（ ）
| A． | 、（0，0 ） | B． | （1-$\sqrt{2}$，0）或（$\sqrt{2}+$1，0） | C． | 、（$\sqrt{2}$+1，0 ） | D． | 、（-$\sqrt{2}$-1，0）或（-$\sqrt{2}$+1，0） |