题目内容
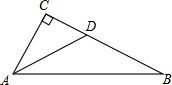 如图,在△ABC中,∠ACB=90°,AD平分∠CAB交CB于D,CD=3,BD=5,求AD的长.
如图,在△ABC中,∠ACB=90°,AD平分∠CAB交CB于D,CD=3,BD=5,求AD的长.考点:角平分线的性质,勾股定理
专题:
分析:首先过D作DE⊥AB,根据角平分线的性质可得CD=DE=3,再根据把勾股定理计算出BE长,再设AC=x,则AE=x,AB=x+4,再次利用勾股定理计算出AC长,再在△ACD中利用勾股定理计算出AD长即可.
解答: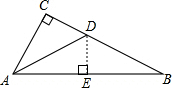 解:过D作DE⊥AB,
解:过D作DE⊥AB,
∵AD平分∠CAB,
∴∠C=∠DEA=90°,CD=DE=3,
∵BD=5,
∴EB=
=4,
在Rt△ACD和Rt△AED中
,
∴Rt△ACD≌Rt△AED(HL),
∴AE=AC,
设AC=x,则AE=x,AB=x+4,
x2+82=(x+4)2,
解得:x=6,
∴AD=
=3
.
 解:过D作DE⊥AB,
解:过D作DE⊥AB,∵AD平分∠CAB,
∴∠C=∠DEA=90°,CD=DE=3,
∵BD=5,
∴EB=
| 52-32 |
在Rt△ACD和Rt△AED中
|
∴Rt△ACD≌Rt△AED(HL),
∴AE=AC,
设AC=x,则AE=x,AB=x+4,
x2+82=(x+4)2,
解得:x=6,
∴AD=
| 62+32 |
| 5 |
点评:此题主要考查了角平分线的性质和勾股定理,关键是掌握角的平分线上的点到角的两边的距离相等.

练习册系列答案
相关题目
若两数x与y的和为12,则下列说法正确的是( )
| A、x=1,y=11时,xy最小 |
| B、x=2,y=10时,xy最大 |
| C、x=3,y=9时,xy最大 |
| D、x=6,y=6时,xy最大 |
有理数a在数轴上的位置如图,则下列各式中正确的是( )


| A、a+3>0 | B、a+3<0 |
| C、a-3>0 | D、a>-3 |
 已知,平面直角坐标系中,直线ABy=-x-
已知,平面直角坐标系中,直线ABy=-x-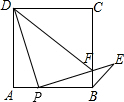 如图,点P是正方形ABCD边AB上的一点(不与A、B重合),连接PD,并将线段PD绕点P顺时针旋转得到线段PE,PE交边BC于点F,连接BE、DF,∠CBE=45°,求证:DP⊥PE.
如图,点P是正方形ABCD边AB上的一点(不与A、B重合),连接PD,并将线段PD绕点P顺时针旋转得到线段PE,PE交边BC于点F,连接BE、DF,∠CBE=45°,求证:DP⊥PE.