题目内容
解方程:
+
=7.
| 2(x2+1) |
| x+1 |
| 6(x+1) |
| x2+1 |
考点:换元法解分式方程
专题:
分析:换元法即是整体思想的考查,解题的关键是找到这个整体,此题的整体是
,设
=y,换元后整理即可求得.
| x2+1 |
| x+1 |
| x2+1 |
| x+1 |
解答:解:设
=y,原方程变形为2y+
=7,
整理得2y2-7y+6=0,
(y-2)(2y-3)=0,
y-2=0或2y-3=0,
解得y1=2,y2=
,
当y=2时,
=2,解得x2-2x-1=0,解得x1=1+
,x2=1-
;
当y=
时,
=
,解得x2-2x-1=0,解得x3=
,x4=
;
∴分式方程的解为:x1=1+
,x2=1-
;x3=
,x4=
.
| x2+1 |
| x+1 |
| 6 |
| y |
整理得2y2-7y+6=0,
(y-2)(2y-3)=0,
y-2=0或2y-3=0,
解得y1=2,y2=
| 3 |
| 2 |
当y=2时,
| x2+1 |
| x+1 |
| 2 |
| 2 |
当y=
| 3 |
| 2 |
| x2+1 |
| x+1 |
| 3 |
| 2 |
3+
| ||
| 4 |
3-
| ||
| 4 |
∴分式方程的解为:x1=1+
| 2 |
| 2 |
3+
| ||
| 4 |
3-
| ||
| 4 |
点评:本题考查了用换元法解分式方程,用换元法解分式方程是常用方法之一,它能够把一些分式方程化繁为简,化难为易.

练习册系列答案
相关题目
 如图,经过折叠可以围成一个
如图,经过折叠可以围成一个 已知△ABC和点O,把△ABC绕点O顺时针旋转90°,得到△A1B1C1,在网格中画出△A1B1C1.
已知△ABC和点O,把△ABC绕点O顺时针旋转90°,得到△A1B1C1,在网格中画出△A1B1C1.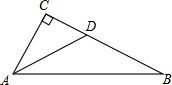 如图,在△ABC中,∠ACB=90°,AD平分∠CAB交CB于D,CD=3,BD=5,求AD的长.
如图,在△ABC中,∠ACB=90°,AD平分∠CAB交CB于D,CD=3,BD=5,求AD的长.