题目内容

10．在平面直角坐标系中，对于任何实数x，点P（x，x2-4x+3）不可能在哪个象限？为什么？

分析 分x是正数和负数两种情况判断出纵坐标的正负情况，再根据各象限内点的坐标特征解答．

解答 解：x是正数时，x2-4x+3=（x-2）2-1，
既可以是正数也可以是负数，
所以，点P可以在第一象限，也可以在第四象限，
x是负数时，x2-4x+3=x2+（-4x）+3＞0，
所以，点P在第二象限，
综上所述，点P不可能在第三象限内．

点评 本题考查了各象限内点的坐标的符号特征，记住各象限内点的坐标的符号是解决的关键，四个象限的符号特点分别是：第一象限（+，+）；第二象限（-，+）；第三象限（-，-）；第四象限（+，-），本题难点在于判断出纵坐标的正负情况．

练习册系列答案
相关题目
20．解下列方程组：
（1）$\left\{\begin{array}{l}{x+y=3}\\{2x-y=6}\end{array}\right.$
（2）$\left\{\begin{array}{l}{x-1=y+5}\\{x+5=5（y-1）}\end{array}\right.$．
1．一个两位数，个位上的数字比十位数的数字大2．且这个两位数在20到40之间，则这个两位数是24或35．
18．计算：
（1）$\sqrt{0.04}+\root{3}{-27}+\sqrt{{{（-2）}^2}}$
（2）|-$\sqrt{2}$|+|$\sqrt{2}-\sqrt{3}$|
5．认真阅读下面的材料，完成有关问题．
材料：在学习绝对值时，老师教过我们绝对值的几何含义，如|5-3|表示5、3在数轴上对应的两点之间的距离；|5+3|=|5-（-3）|，所以|5+3|表示5、-3在数轴上对应的两点之间的距离；|5|=|5-0|，所以|5|表示5在数轴上对应的点到原点的距离．一般地，点A、B在数轴上分别表示有理数a、b，那么A、B之间的距离可表示为|a-b|．
问题（1）：点A、B、C在数轴上分别表示有理数x、-2、1，那么A到B的距离与A到C的距离之和可表示为|x+2|+|x-1|（用含绝对值的式子表示）．
问题（2）：利用数轴探究：①找出满足|x-3|+|x+1|=6的x的所有值是-2，4，②设|x-3|+|x+1|=p，当x的值取在不小于-1且不大于3的范围时，p的值是不变的，而且是p的最小值，这个最小值是4；当x的值取在不小于0且不大于2的范围时，|x|+|x-2|的最小值是2．
问题（3）：求|x-3|+|x-2|+|x+1|的最小值以及此时x的值．
问题（4）：若|x-3|+|x-2|+|x|+|x+1|≥a对任意的实数x都成立，求a的取值．
15．在平面直角坐标系中，如果横坐标与纵坐标都是整数，我们把这样的点称为整点，已知（a，b）是整点，且在第二象限，已知点P（2a-5，3b-6）先向右平移10个单位，再向下平移2个单位，得到点Q，点Q在第四象限．则这样的整点有几个？
2．一列快车从甲地驶往乙地，一列慢车从乙地驶往甲地，两车同时出发，设慢车行驶的时间为x（h），两车之间的距离为y（km），图中的折线表示y与x之间的函数关系．根据图象信息解答：当出发几个小时后，两车相距为270km？
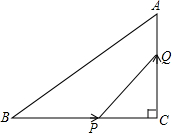16．如图，△ABC中，∠C=90°，AC=3cm，BC=4cm，动点P从点B出发以2cm/s的速度向点C移动，同时动点Q从C出发以1cm/s的速度向点A移动，设它们的运动时间为t．
（1）t为何值时，△CPQ的面积等于△ABC面积的$\frac{1}{8}$？
（2）运动几秒时，△CPQ与△CBA相似？
（3）在运动过程中，PQ的长度能否为1cm？试说明理由．
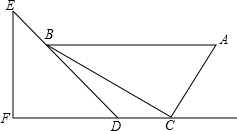17．一副直角三角板如图放置，点C在FD的延长线上，AB∥CF，∠F=∠ACB=90°，∠E=45°，∠A=60°，AC=10．
（1）求直线AB与CF之间的距离；
（2）求CD的长．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网