题目内容
17.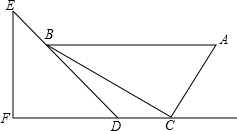 一副直角三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A=60°,AC=10.
一副直角三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A=60°,AC=10.(1)求直线AB与CF之间的距离;
(2)求CD的长.
分析 (1)过点B作BM⊥FD于点M,先解直角△ACB中,得出BC=AC×tan∠A=10$\sqrt{3}$,由AB∥CF,得出∠BCM=∠ABC=30°,再解直角△BCM,得出BM=BC×sin∠BCM=5$\sqrt{3}$,CM=BC×cos∠BCM=15,即直线AB与CF之间的距离为5$\sqrt{3}$;
(2)在△EFD中可求出∠EDF=45°,那么MD=BM=5$\sqrt{3}$,再根据CD=CM-MD即可得出答案.
解答 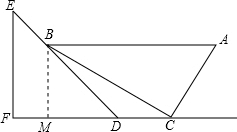 解:(1)过点B作BM⊥FD于点M,
解:(1)过点B作BM⊥FD于点M,
∵在△ACB中,∠ACB=90°,∠A=60°,AC=10,
∴∠ABC=30°,BC=10×tan60°=10$\sqrt{3}$,
∵AB∥CF,
∴∠BCM=∠ABC=30°.
∵在直角△BCM中,∠BMC=90°,∠BCM=30°,
∴BM=BC×sin30°=10$\sqrt{3}$×$\frac{1}{2}$=5$\sqrt{3}$,CM=BC×cos30°=15,
即直线AB与CF之间的距离为5$\sqrt{3}$;
(2)∵在△EFD中,∠F=90°,∠E=45°,
∴∠EDF=45°,
∴MD=BM=5$\sqrt{3}$,
∴CD=CM-MD=15-5$\sqrt{3}$.
点评 本题考查了解直角三角形及平行线的性质,难度适中,解答此类题目的关键根据题意建立三角形利用所学的三角函数的关系进行解答.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
2.下列说法正确的是( )
| A. | 为了了解全国中学生每天体育锻炼的时间,应采用普查的方式 | |||||||||||||
| B. | 甲组数据的方差${S_甲}^2$=0.03,乙组数据的方差是${S_乙}^2$=0.2,则乙组数据比甲组数据稳定 | |||||||||||||
| C. | 广州市明天一定会下雨 | |||||||||||||
| D. | 某班学生数学成绩统计如下,则该班学生数学成绩的众数和中位数分别是80分,80分
|
9.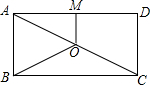 如图,O是矩形ABCD的对角线AC的中点,M是AD的中点,若AB=5,AD=12,则四边形ABOM的周长为( )
如图,O是矩形ABCD的对角线AC的中点,M是AD的中点,若AB=5,AD=12,则四边形ABOM的周长为( )
 如图,O是矩形ABCD的对角线AC的中点,M是AD的中点,若AB=5,AD=12,则四边形ABOM的周长为( )
如图,O是矩形ABCD的对角线AC的中点,M是AD的中点,若AB=5,AD=12,则四边形ABOM的周长为( )| A. | 17 | B. | 18 | C. | 19 | D. | 20 |
6.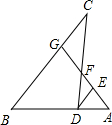 如图,点G、F分别是△BCD的边BC、CD上的点,BD的延长线与GF的延长线相交于点A,DE∥BC交GA于点E,则下列结论错误的是( )
如图,点G、F分别是△BCD的边BC、CD上的点,BD的延长线与GF的延长线相交于点A,DE∥BC交GA于点E,则下列结论错误的是( )
 如图,点G、F分别是△BCD的边BC、CD上的点,BD的延长线与GF的延长线相交于点A,DE∥BC交GA于点E,则下列结论错误的是( )
如图,点G、F分别是△BCD的边BC、CD上的点,BD的延长线与GF的延长线相交于点A,DE∥BC交GA于点E,则下列结论错误的是( )| A. | $\frac{AD}{BD}$=$\frac{AE}{EG}$ | B. | $\frac{DE}{CG}$=$\frac{DF}{CF}$ | C. | $\frac{AE}{AG}$=$\frac{DE}{BC}$ | D. | $\frac{AD}{AB}$=$\frac{DE}{BG}$ |
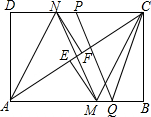 如图,在矩形ABCD中,把∠B、∠D分别翻折,使点B、D分别落在对角线BC上的点E、F处,折痕分别为CM、AN.连接MF、NE. P、Q是矩形的边CD、AB上的两点,连结PQ、CQ、MN.若PQ=CQ,PQ∥MN,且AB=4,BC=3,则PC的长度是2.
如图,在矩形ABCD中,把∠B、∠D分别翻折,使点B、D分别落在对角线BC上的点E、F处,折痕分别为CM、AN.连接MF、NE. P、Q是矩形的边CD、AB上的两点,连结PQ、CQ、MN.若PQ=CQ,PQ∥MN,且AB=4,BC=3,则PC的长度是2.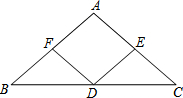 已知:如图,D是△ABC的边BC的中点,DE⊥AC、DF⊥AB,垂足分别是E、F,且BF=CE,
已知:如图,D是△ABC的边BC的中点,DE⊥AC、DF⊥AB,垂足分别是E、F,且BF=CE,