题目内容
1.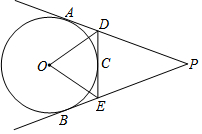 如图,PA、PB、DE分别切⊙O于点A、B、C,DE交PA、PB于点D、E,若∠P=40°,则∠DOE=70°.
如图,PA、PB、DE分别切⊙O于点A、B、C,DE交PA、PB于点D、E,若∠P=40°,则∠DOE=70°.
分析 分别连接OA、OB、OC,由四边形内角和可求得∠AOB,再根据切线和定理可求得∠DOC+∠EOC,则可求得答案.
解答  解:
解:
如图,分别连接OA、OB、OC,
∵PA、PB、DE分别切⊙O于点A、B、C,
∴∠OAP=∠OBP=90°,
∴∠AOB=360°-90°-90°-∠P=140°,
∵DA、DC是⊙O的切线,
∴OD平分∠AOC,
∴∠DOC=$\frac{1}{2}$∠AOC,
同理可得∠EOC=$\frac{1}{2}$∠BOC,
∴∠DOE=∠DOC+∠EOC=$\frac{1}{2}$(∠AOC+∠BOC)=$\frac{1}{2}$∠AOB=70°,
故答案为:70°.
点评 本题主要考查切线的性质及切线长定理,根据切线长定理求得∠DOE=$\frac{1}{2}$∠AOB是解题的关键,注意整体思想的应用.

练习册系列答案
相关题目
6.一元二次方程3x(x+1)=3x+3的解为( )
| A. | x=1 | B. | x=-1 | C. | x1=1,x2=-1 | D. | x1=0,x2=-1 |
 如图,在△ABC中,M,N分别是边AB,AC的中点,则△AMN的面积与四边形MBCN的面积比为1:3.
如图,在△ABC中,M,N分别是边AB,AC的中点,则△AMN的面积与四边形MBCN的面积比为1:3.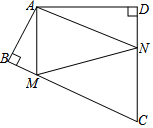 如图,四边形ABCD中,∠BAD=120°,∠B=∠D=90°,AB=1,AD=2,在BC、CD上分别找一点M、N,使△AMN周长最小,则最小值为2$\sqrt{7}$.
如图,四边形ABCD中,∠BAD=120°,∠B=∠D=90°,AB=1,AD=2,在BC、CD上分别找一点M、N,使△AMN周长最小,则最小值为2$\sqrt{7}$.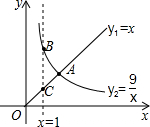 函数y1=x(x≥0),y2=$\frac{9}{x}$(x>0)的图象如图所示,则结论:
函数y1=x(x≥0),y2=$\frac{9}{x}$(x>0)的图象如图所示,则结论: