题目内容
13. 若BE为等腰Rt△OAB的中线,OF⊥BE于F,交AB于G,连EG.
若BE为等腰Rt△OAB的中线,OF⊥BE于F,交AB于G,连EG.(1)证明:OG+EG=BE;
(2)求证:∠OEF=∠AEG.
分析 (1)过点A作AC⊥AO交OG的延长线于点C,首先求出∠ACO=∠OEF,利用ASA证明△OAC≌△BOE,于是得到BE=OC=OG+CG,OE=AC,进而利用SAS证明△EAG≌△CAG,于是得到CG=EG,即可得到结论;
(2)根据△EAG≌△CAG得到∠ACO=∠AEG,再利用角之间的等量关系得到结论.
解答  证明:(1)过点A作AC⊥AO交OG的延长线于点C,
证明:(1)过点A作AC⊥AO交OG的延长线于点C,
∵△AOB为等腰直角三角形,
∴AO=BO,∠AOB=∠OAC=90°,
∵∠ACO+∠AOC=∠OEF+∠AOC,
∴∠ACO=∠OEF,
在△OAC和△BOE中,
∵$\left\{\begin{array}{l}{∠CAO=∠EOB}\\{AO=BO}\\{∠AOC=∠OBE}\end{array}\right.$,
∴△OAC≌△BOE,
∴BE=OC=OG+CG,OE=AC,
∵OE=AE,
∴AE=AC,
∵∠OAC=90°,∠OAB=45°,
∴∠OAB=∠CAG=45°,
在△EAG和△CAG中,
∵$\left\{\begin{array}{l}{AE=AC}\\{∠EAG=∠CAG}\\{AG=AG}\end{array}\right.$
∴△EAG≌△CAG,
∴CG=EG,
∴OG+EG=BE;
(2)∵△EAG≌△CAG,
∴∠ACO=∠AEG,
∵∠ACO=∠OEF,
∴∠OEF=∠AEG.
点评 本题主要考查了全等三角形的判定与性质的知识,解答本题的关键是利用ASA证明△OAC≌△BOE,利用SAS证明△EAG≌△CAG,此题有一定的难度.

练习册系列答案
相关题目

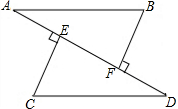 如图,已知AE=DF,AB∥CD,CE⊥AD,BF⊥AD.求证:
如图,已知AE=DF,AB∥CD,CE⊥AD,BF⊥AD.求证: 如图,在等腰直角三角形ABC中,∠ACB=90°,点D在边AB上,连接CD,过点A,C分别作AB,CD的垂线,两垂线交于点E,连接DE.
如图,在等腰直角三角形ABC中,∠ACB=90°,点D在边AB上,连接CD,过点A,C分别作AB,CD的垂线,两垂线交于点E,连接DE. 如图,在△ABC中,AD是BC边上的高,∠ABC=2∠C,E是AC的中点,ED的延长线交AB的延长线于点F.
如图,在△ABC中,AD是BC边上的高,∠ABC=2∠C,E是AC的中点,ED的延长线交AB的延长线于点F. 如图,在△ABC中,∠ACB=90°,AC=BC,BE是中线,CG平分∠ACB交BE于点G,F为AB边上一点,且∠ACF=∠CBG.
如图,在△ABC中,∠ACB=90°,AC=BC,BE是中线,CG平分∠ACB交BE于点G,F为AB边上一点,且∠ACF=∠CBG.