Question

8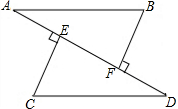．如图，已知AE=DF，AB∥CD，CE⊥AD，BF⊥AD．求证：
（1）∠A=∠D；
（2）BF=CE．

Answer 1

分析 （1）由AB∥CD根据两直线平行内错角相等可得；
（2）由AE=DF知AF=DE，根据CE⊥AD、BF⊥AD知∠AFB=∠DEC，证△ABF≌△DCE即可．

解答 证明：（1）∵AB∥CD，
∴∠A=∠D；
（2）∵AE=DF，
∴AE+EF=DF+EF，即AF=DE，
又∵CE⊥AD，BF⊥AD，
∴∠AFB=∠DEC=90°，
在△ABF和△DCE中，
∵$\left\{\begin{array}{l}{∠A=∠D}\\{AF=DE}\\{∠AFB=∠DEC}\end{array}\right.$，
∴△ABF≌△DCE（ASA），
∴BF=CE．

点评 本题主要考查平行线的性质和全等三角形的判定与性质，证明△ABF≌△DCE是关键．