题目内容
 如图,△AOB为等腰三角形,顶点A的坐标(2,
如图,△AOB为等腰三角形,顶点A的坐标(2,| 5 |
考点:坐标与图形变化-旋转,等腰三角形的性质
专题:
分析:过点A作AC⊥OB于C,过点O′作O′D⊥A′B于D,根据点A的坐标求出OC、AC,再利用勾股定理列式计算求出OA,根据等腰三角形三线合一的性质求出OB,根据旋转的性质可得BO′=OB,∠A′BO′=∠ABO,然后解直角三角形求出O′D、BD,再求出OD,然后写出点O′的坐标即可.
解答:解:如图,
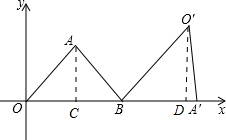
过点A作AC⊥OB于C,过点O′作O′D⊥A′B于D,
∵A(2,
),
∴OC=2,AC=
,
由勾股定理得,OA=
=
=3,
∵△AOB为等腰三角形,OB是底边,
∴OB=2OC=2×2=4,
由旋转的性质得,BO′=OB=4,∠A′BO′=∠ABO,
∴O′D=4×
=
,
BD=4×
=
,
∴OD=OB+BD=4+
=
,
∴点O′的坐标为(
,
),
故答案为:(
,
).

过点A作AC⊥OB于C,过点O′作O′D⊥A′B于D,
∵A(2,
| 5 |
∴OC=2,AC=
| 5 |
由勾股定理得,OA=
| OC2+AC2 |
22+(
|
∵△AOB为等腰三角形,OB是底边,
∴OB=2OC=2×2=4,
由旋转的性质得,BO′=OB=4,∠A′BO′=∠ABO,
∴O′D=4×
| ||
| 3 |
4
| ||
| 3 |
BD=4×
| 2 |
| 3 |
| 8 |
| 3 |
∴OD=OB+BD=4+
| 8 |
| 3 |
| 20 |
| 3 |
∴点O′的坐标为(
| 20 |
| 3 |
4
| ||
| 3 |
故答案为:(
| 20 |
| 3 |
4
| ||
| 3 |
点评:本题考查了坐标与图形变化-旋转,主要利用了勾股定理,等腰三角形的性质,解直角三角形,熟记性质并作辅助线构造出直角三角形是解题的关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
下列说法正确的是( )
A、在球的体积公V=
| ||||
| B、若变量x、y满足y2=x,则y是x的函数 | ||||
C、在圆锥的体积公式V=
| ||||
D、若变量x、y满足y=-
|
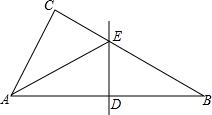 如图,在△ABC中,∠C=90°,E为BC边上一点,将△CAE沿AE折叠,C的对应点D恰好落在AB的中点上,求∠B的度数.
如图,在△ABC中,∠C=90°,E为BC边上一点,将△CAE沿AE折叠,C的对应点D恰好落在AB的中点上,求∠B的度数.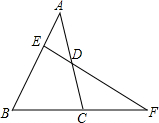 如图,过△ABC的边AC的中点D作直线交AB于E,交BC的延长线于F.
如图,过△ABC的边AC的中点D作直线交AB于E,交BC的延长线于F. 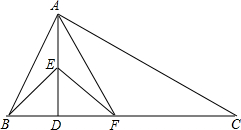 如图,在△ABC中,∠BAC=90°,AD是斜边BC上的高,∠ABD的平分线交AD于点E,∠CAD的平分线交CD于点F,连接EF.求证:EF∥AC.
如图,在△ABC中,∠BAC=90°,AD是斜边BC上的高,∠ABD的平分线交AD于点E,∠CAD的平分线交CD于点F,连接EF.求证:EF∥AC.