题目内容
1.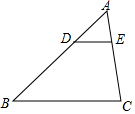 如图,在△ABC中,点D、E分别在AB、AC上,且DE∥BC,那么下列说法中错误的是( )
如图,在△ABC中,点D、E分别在AB、AC上,且DE∥BC,那么下列说法中错误的是( )| A. | $\frac{AD}{BD}$=$\frac{AE}{EC}$ | B. | $\frac{AD}{AB}$=$\frac{AE}{AC}$ | C. | $\frac{DE}{BC}$=$\frac{AD}{DB}$ | D. | $\frac{DE}{BC}$=$\frac{AE}{AC}$ |
分析 直接利用平行线分线段成比例定理结合相似三角形的性质得出答案.
解答 解:∵DE∥BC,
∴$\frac{AD}{BD}$=$\frac{AE}{EC}$,故选项A正确,不合题意;
∵DE∥BC,
∴△ADE∽△ABC,
∴$\frac{AD}{AB}$=$\frac{AE}{AC}$=$\frac{DE}{BC}$,
故选项B正确,不合题意;
则选项C错误,符合题意;
选项D正确,不合题意.
故选:C.
点评 此题主要考查了平行线分线段成比例定理和相似三角形的性质,正确掌握相似三角形的性质是解题关键.

练习册系列答案
相关题目
12.已知:非零向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$,在下列条件中,不能判定$\overrightarrow{a}$∥$\overrightarrow{b}$的是( )
| A. | $\overrightarrow{a}$∥$\overrightarrow{c}$,$\overrightarrow{b}$∥$\overrightarrow{c}$ | B. | $\overrightarrow{a}$=3$\overrightarrow{c}$,$\overrightarrow{b}$=-$\overrightarrow{c}$ | C. | $\overrightarrow{a}$=-5$\overrightarrow{b}$ | D. | $|{\overrightarrow a}|=2|{\overrightarrow b}|$ |
6.下列命题中,真命题是( )
| A. | 垂直于同一条直线的两条直线互相平行 | |
| B. | 两条平行直线被第三条直线所截,则一组同旁内角的平分线互相垂直 | |
| C. | 三角形的一个外角等于两个内角的和 | |
| D. | 等边三角形既是中心对称图形,又是轴对称图形 |
13.0.000 000 275用科学记数法表示为( )
| A. | 2.75×10-8 | B. | 2.75×10-7 | C. | 2.75×10-6 | D. | 2.75×10-5 |
10.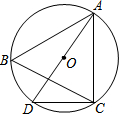 如图,⊙O是△ABC的外接圆,AD是⊙O的直径,连接CD,若⊙O的半径r=5,AC=5$\sqrt{3}$,则∠B的度数是( )
如图,⊙O是△ABC的外接圆,AD是⊙O的直径,连接CD,若⊙O的半径r=5,AC=5$\sqrt{3}$,则∠B的度数是( )
 如图,⊙O是△ABC的外接圆,AD是⊙O的直径,连接CD,若⊙O的半径r=5,AC=5$\sqrt{3}$,则∠B的度数是( )
如图,⊙O是△ABC的外接圆,AD是⊙O的直径,连接CD,若⊙O的半径r=5,AC=5$\sqrt{3}$,则∠B的度数是( )| A. | 30° | B. | 45° | C. | 50° | D. | 60° |
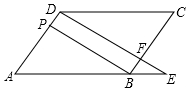 如图,在?ABCD中,F是BC上的一点,直线DF与AB的延长线相交于点E,BP∥DF,且与AD相交于点P,则图中相似三角形的组数为( )
如图,在?ABCD中,F是BC上的一点,直线DF与AB的延长线相交于点E,BP∥DF,且与AD相交于点P,则图中相似三角形的组数为( )