题目内容
9.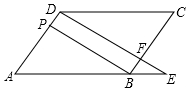 如图,在?ABCD中,F是BC上的一点,直线DF与AB的延长线相交于点E,BP∥DF,且与AD相交于点P,则图中相似三角形的组数为( )
如图,在?ABCD中,F是BC上的一点,直线DF与AB的延长线相交于点E,BP∥DF,且与AD相交于点P,则图中相似三角形的组数为( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
分析 可利用平行于三角形的一边的直线与其它两边相交,所构成的三角形与原三角形相似判断即可.
解答 解:∵BP∥DF,
∴△ABP∽△AED;
∴四边形ABCD是平行四边形,
∴DC∥AB,BC∥AD,
∴△CDF∽△BEF,△EFB∽△EDA;
同理,△CDF∽△AED,△CDF∽△ABP,△ABP∽BEF
故选D.
点评 本题考查了相似三角形的判定与性质:平行于三角形的一边的直线与其他两边相交,所构成的三角形与原三角形相似.

练习册系列答案
相关题目
19.如图,从边长为(a+4)cm的正方形纸片中剪去一个边长为(a+1)cm的正方形(a>0),剩余部分沿虚线又剪拼成一个矩形(不重叠无缝隙),则矩形的面积为( )
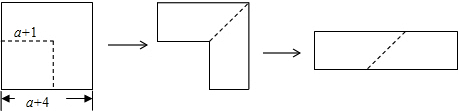

| A. | (6a+15)cm2 | B. | (3a+15)cm2 | C. | (6a+9)cm2 | D. | (2a2+5a)cm2 |
17.近似数-0.03750的有效数字有( )个.
| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
4. 如图,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB,交BC于D,DE⊥AB于E,且AE=6cm,则△ABC的周长为( )
如图,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB,交BC于D,DE⊥AB于E,且AE=6cm,则△ABC的周长为( )
 如图,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB,交BC于D,DE⊥AB于E,且AE=6cm,则△ABC的周长为( )
如图,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB,交BC于D,DE⊥AB于E,且AE=6cm,则△ABC的周长为( )| A. | 24cm | B. | (12+6$\sqrt{2}$)cm | C. | 10cm | D. | (8+6$\sqrt{3}$)cm |
1.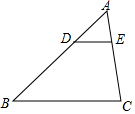 如图,在△ABC中,点D、E分别在AB、AC上,且DE∥BC,那么下列说法中错误的是( )
如图,在△ABC中,点D、E分别在AB、AC上,且DE∥BC,那么下列说法中错误的是( )
 如图,在△ABC中,点D、E分别在AB、AC上,且DE∥BC,那么下列说法中错误的是( )
如图,在△ABC中,点D、E分别在AB、AC上,且DE∥BC,那么下列说法中错误的是( )| A. | $\frac{AD}{BD}$=$\frac{AE}{EC}$ | B. | $\frac{AD}{AB}$=$\frac{AE}{AC}$ | C. | $\frac{DE}{BC}$=$\frac{AD}{DB}$ | D. | $\frac{DE}{BC}$=$\frac{AE}{AC}$ |
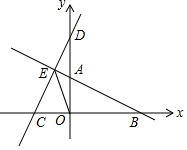 如图,直线y=-$\frac{1}{2}$x+1交y轴于A点,交x轴于B点,将Rt△AOB绕O点逆时针旋转90°,得到Rt△COD,直线AB交直线CD于E点.
如图,直线y=-$\frac{1}{2}$x+1交y轴于A点,交x轴于B点,将Rt△AOB绕O点逆时针旋转90°,得到Rt△COD,直线AB交直线CD于E点.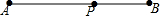 已知线段AB及AB上一点P,当点P满足下列哪一种关系时,点P为AB的黄金分割点( )
已知线段AB及AB上一点P,当点P满足下列哪一种关系时,点P为AB的黄金分割点( )