题目内容
8.如图1,在平面直角坐标系中,已知点A(0,6).点B(6,6),点C(6,0),点D是射线OA(O,A除外)上的动点,点E是O点关于直线CD的对称点,延长DE交直线AB于点F,连结CF.(1)某探究小组发现:当点D在线段OA上时,有①EF=BF;②∠DCF=45°,请选择其中一个证明.
(2)当AD=2时,求点F的坐标.
(3)探究小组又发现:如图2.当点D在线段OA上时,射线CD、CF与射线OB分别交于点M,N,线段OM,MN,BN之间除了存在OM+MN+NB=6$\sqrt{2}$外,还存在着另外的等式关系,你能找到并写出这个等式吗?当点D不在线段OA上时,这两个等式是否仍然成立?请说明理由.

分析 (1)只要证明Rt△CFE≌Rt△CFB,推出EF=BF,∠FCE=∠FCB,推出∠DCF=∠DCE+∠FCE=$\frac{1}{2}$∠ECO+$\frac{1}{2}$∠ECB=$\frac{1}{2}$∠OCB=45°,由此即可解决问题;
(2)由AD=2,推出OD=DE=4,设EFF=FB=x,则AF=6-x,在Rt△ADF中,根据AD2+AF2=DF2可得22+(6-x)2=(4+x)2,解方程即可解决问题;
(3)①如图2中,当当D在线段OA上时,结论:MN2=OM2+NB2.只要证明△CNM≌△CNP,推出MN=PN,由∠OBC=∠CBP=45°,推出∠MBP=90°,可得BN2+BP2=PN2,由此即可解决问题;
②如图3中,当点D在线段OA的延长线上时,结论不变.证明方法类似;
解答 (1)证明:如图1中,
∵O、E关于CD对称,
∴OD=DE,OC=CE=CB,∠DCE=∠DCO,
∵CF=CF,
∴Rt△CFE≌Rt△CFB,
∴EF=BF,∠FCE=∠FCB,
∴∠DCF=∠DCE+∠FCE=$\frac{1}{2}$∠ECO+$\frac{1}{2}$∠ECB=$\frac{1}{2}$∠OCB=45°,
∴FE=FB,∠DCF=45°.
(2)解:如图1中,
∵AD=2,
∴OD=DE=4,设EFF=FB=x,则AF=6-x,
在Rt△ADF中,∵AD2+AF2=DF2
∴22+(6-x)2=(4+x)2,
∴x=$\frac{6}{5}$.
(3)解:①如图2中,当当D在线段OA上时,结论:MN2=OM2+NB2.
理由:将△OCM绕点C顺时针旋转90°,得到△CBP.
∵∠DCF=45°,
∴∠OCM+∠BCN=45°,
∵∠OCM=∠BCP,
∴∠NCB+∠BCP=45°,
∴∠MCN=∠NCP,∵CN=CN,CM=CP,
∴△CNM≌△CNP,
∴MN=PN,
∵∠OBC=∠CBP=45°,
∴∠MBP=90°,
∴BN2+BP2=PN2,
∴MN2=OM2+NB2.
②如图3中,当点D在线段OA的延长线上时,第一个结论变了:OM+MN-BN=6$\sqrt{2}$.理由:OM+MN-BN=OB=6$\sqrt{2}$.
第二个结论不变,理由如下:
理由:将△OCM绕点C顺时针旋转90°,得到△CBP.
易证∠DCO=∠DCE,∠FCE=∠FCB,
∴∠DCF=∠DCE-∠FCE=$\frac{1}{2}$∠OCE-$\frac{1}{2}$∠BCE=$\frac{1}{2}$(∠OCE-∠BCE)=45°,
∴∠OCM-∠BCN=45°,
∵∠OCM=∠BCP,
∴∠NCP=∠BCP-∠BCN=45°,
∴∠MCN=∠NCP=45°,
∵CN=CN,CM=CP,
∴△CNM≌△CNP,
∴MN=PN,
∵∠OBC=∠CBP=45°,
∴∠MBP=90°,
∴BN2+BP2=PN2,
∴MN2=OM2+NB2.
点评 本题考查一次函数综合题、正方形的性质、勾股定理、全等三角形的判定和性质、对称轴变换、旋转变换等知识,解题的关键是学会利用旋转法添加辅助线,构造全等三角形解决问题,属于中考压轴题.

 科学实验活动册系列答案
科学实验活动册系列答案| A. | 调查一批电脑的使用寿命情况 | |
| B. | 调查全国足球迷的身体健康状况 | |
| C. | 调查重庆市中小学生课外阅读情况 | |
| D. | 为保证“神州十一号”载人飞船的成功发射,对其零部件的检查 |
| A. | a<b<m<n | B. | b<a<n<m | C. | a<m<n<b | D. | m<a<b<n |
| A. | $\frac{4}{5}$ | B. | $\frac{5}{4}$ | C. | -$\frac{4}{5}$ | D. | -$\frac{5}{4}$ |
 如图,△ABC三个顶点分别在反比例函数y=$\frac{1}{x}$,y=$\frac{k}{x}$的图象上,若∠C=90°,AC∥y轴,BC∥x轴,S△ABC=8,则k的值为( )
如图,△ABC三个顶点分别在反比例函数y=$\frac{1}{x}$,y=$\frac{k}{x}$的图象上,若∠C=90°,AC∥y轴,BC∥x轴,S△ABC=8,则k的值为( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
| A. | 向上平移2个单位 | B. | 向下平移2个单位 | C. | 向右平移2个单位 | D. | 向左平移2个单位 |
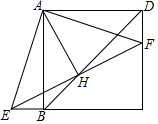 已知四边形ABCD是正方形,F、E分别是DC和CB延长线上的点,且DF=BE,连接AE、AF、EF
已知四边形ABCD是正方形,F、E分别是DC和CB延长线上的点,且DF=BE,连接AE、AF、EF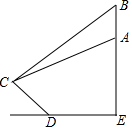 最近央视纪录片《航拍中国》中各地的美景震撼了全国观众,如图是航拍无人机从A点俯拍在坡比为3:4的斜坡CD上的景点C,此时的俯角为30°,为取得更震撼的拍摄效果,无人机升高200米到达B点,此时的俯角变为45°.已知无人机与斜坡CD的坡底D的水平距离DE为400米,则斜坡CD的长度为( )米(精确到0.1米,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
最近央视纪录片《航拍中国》中各地的美景震撼了全国观众,如图是航拍无人机从A点俯拍在坡比为3:4的斜坡CD上的景点C,此时的俯角为30°,为取得更震撼的拍摄效果,无人机升高200米到达B点,此时的俯角变为45°.已知无人机与斜坡CD的坡底D的水平距离DE为400米,则斜坡CD的长度为( )米(精确到0.1米,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)