题目内容
先阅读命题及证明思路,再解答下列问题.
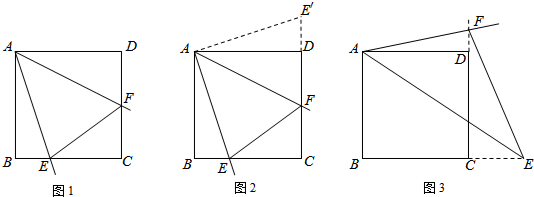
命题:如图1,在正方形ABCD中,已知:∠EAF=45°,角的两边AE、AF分别与BC、CD相交于点E、F,连接EF.求证:EF=BE+DF.
证明思路:
如图2,将△ABE绕点A逆时针旋转90°至△ADE′.∵AB=AD,∠BAD=90°,∴AB与AD重合.∵∠ADC=∠B=90°,∴∠FDE′=180°,点F、D、E′是一条直线.
根据SAS,得证△AEF≌△AFE′,得EF=E′F=E′D+DF=BE+DF.
(1)特例应用
如图1,命题中,如果BE=2,DF=3,求正方形ABCD的边长.
(2)类比变式
如图3,在正方形ABCD中,已知∠EAF=45°,角的两边AE、AF分别与BC、CD的延长线相交于点E、F,连接EF.写出EF、BE、DF之间的关系式,并证明你的结论.
(3)拓展深入
如图4,在⊙O中,AB、AD是⊙O的弦,且AB=AD,M、N是⊙O上的两点,∠MAN=
∠BAD.
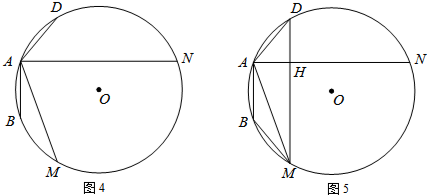
①如图5,连接MN、MD,求证:MH=BM+DH,DM⊥AN;
②若点C在
(点C不与点A、D、N、M重合)上,连接CB、CD分别交AM、AN或其延长线于点E、F,直接写出EF、BE、DF之间的等式关系.
命题:如图1,在正方形ABCD中,已知:∠EAF=45°,角的两边AE、AF分别与BC、CD相交于点E、F,连接EF.求证:EF=BE+DF.
证明思路:
如图2,将△ABE绕点A逆时针旋转90°至△ADE′.∵AB=AD,∠BAD=90°,∴AB与AD重合.∵∠ADC=∠B=90°,∴∠FDE′=180°,点F、D、E′是一条直线.
根据SAS,得证△AEF≌△AFE′,得EF=E′F=E′D+DF=BE+DF.

(1)特例应用
如图1,命题中,如果BE=2,DF=3,求正方形ABCD的边长.
(2)类比变式
如图3,在正方形ABCD中,已知∠EAF=45°,角的两边AE、AF分别与BC、CD的延长线相交于点E、F,连接EF.写出EF、BE、DF之间的关系式,并证明你的结论.
(3)拓展深入
如图4,在⊙O中,AB、AD是⊙O的弦,且AB=AD,M、N是⊙O上的两点,∠MAN=
| 1 |
| 2 |
①如图5,连接MN、MD,求证:MH=BM+DH,DM⊥AN;
②若点C在
 |
| ADM |

考点:圆的综合题,四边形综合题
专题:阅读型,探究型
分析:(1)如图1,设正方形ABCD的边长为x,则有CE=x-2,CF=x-3.由材料可知:EF=BE+DF=5,在Rt△CEF中,运用勾股定理就可解决问题.
(2)仿照材料中的证明思路就可解决问题.
(3)①延长MD到点M′,使得DM′=BM,连接AM′,如图5.仿照材料中的证明思路可证到AM=AM′,∠MAN=∠M′AN,然后利用等腰三角形的性质即可解决问题.②分两种情况讨论:Ⅰ.当点C在
上时,如图6、7;Ⅱ.当点C在
上时,如图8.借鉴①中的证明思路就可得到结论.
(2)仿照材料中的证明思路就可解决问题.
(3)①延长MD到点M′,使得DM′=BM,连接AM′,如图5.仿照材料中的证明思路可证到AM=AM′,∠MAN=∠M′AN,然后利用等腰三角形的性质即可解决问题.②分两种情况讨论:Ⅰ.当点C在
 |
| DNM |
 |
| AD |
解答:解:(1)如图1,
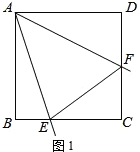
设正方形ABCD的边长为x,则有CE=x-2,CF=x-3.
由材料可知:EF=BE+DF=2+3=5.
在Rt△CEF中,
∵∠C=90°,
∴CE2+CF2=EF2.
∴(x-2)2+(x-3)2=52.
解得:x1=6,x2=-1(舍去)
所以正方形ABCD的边长为6.
(2)EF=BE-DF.
理由如下:
在BC上取一点F′,使得BF′=DF.连接AF′,如图3.
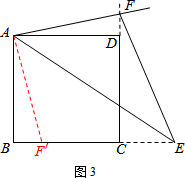
∵四边形ABCD是正方形,
∴AB=AD,∠B=∠BAD=∠ADC=90°.
∴∠ADF=90°=∠B.
在△ABF′和△ADF中,
.
∴△ABF′≌△ADF(SAS).
∴AF′=AF,∠BAF′=∠DAF.
∴∠F′AF=∠BAD=90°.
∵∠EAF=45°,
∴∠F′AE=45°=∠FAE.
在△F′AE和△FAE中,
.
∴△F′AE≌△FAE(SAS).
∴F′E=FE.
∴EF=F′E=BE-BF′=BE-DF.
(3)①延长MD到点M′,使得DM′=BM,连接AM′,如图5.
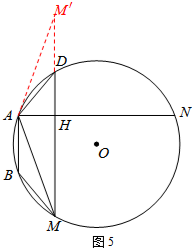
∵∠ADM′+∠ADM=180°,∠ABM+∠ADM=180°,
∴∠ABM=∠ADM′.
在△ABM和△ADM′中,
.
∴△ABM≌△ADM′(SAS).
∴AM=AM′∠BAM=∠DAM′.
∴∠MAM′=∠BAD.
∵∠MAN=
∠BAD,
∴∠MAN=
∠MAM′.
∴∠MAN=∠M′AN.
∵AM=AM′,∠MAN=∠M′AN,
∴MH=M′H,AH⊥MM′.
∴MH=M′H=DM′+DH=BM+DH,DM⊥AN.
②Ⅰ.当点C在
上时,如图6、7.
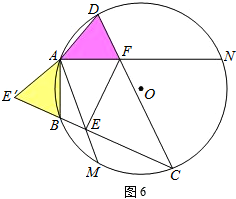
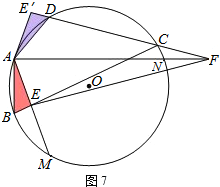
同理可得:EF=BE+DF.
Ⅱ.当点C在
上时,如图8.
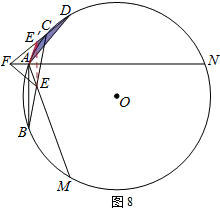
同理可得:EF=DF-BE.

设正方形ABCD的边长为x,则有CE=x-2,CF=x-3.
由材料可知:EF=BE+DF=2+3=5.
在Rt△CEF中,
∵∠C=90°,
∴CE2+CF2=EF2.
∴(x-2)2+(x-3)2=52.
解得:x1=6,x2=-1(舍去)
所以正方形ABCD的边长为6.
(2)EF=BE-DF.
理由如下:
在BC上取一点F′,使得BF′=DF.连接AF′,如图3.

∵四边形ABCD是正方形,
∴AB=AD,∠B=∠BAD=∠ADC=90°.
∴∠ADF=90°=∠B.
在△ABF′和△ADF中,
|
∴△ABF′≌△ADF(SAS).
∴AF′=AF,∠BAF′=∠DAF.
∴∠F′AF=∠BAD=90°.
∵∠EAF=45°,
∴∠F′AE=45°=∠FAE.
在△F′AE和△FAE中,
|
∴△F′AE≌△FAE(SAS).
∴F′E=FE.
∴EF=F′E=BE-BF′=BE-DF.
(3)①延长MD到点M′,使得DM′=BM,连接AM′,如图5.

∵∠ADM′+∠ADM=180°,∠ABM+∠ADM=180°,
∴∠ABM=∠ADM′.
在△ABM和△ADM′中,
|
∴△ABM≌△ADM′(SAS).
∴AM=AM′∠BAM=∠DAM′.
∴∠MAM′=∠BAD.
∵∠MAN=
| 1 |
| 2 |
∴∠MAN=
| 1 |
| 2 |
∴∠MAN=∠M′AN.
∵AM=AM′,∠MAN=∠M′AN,
∴MH=M′H,AH⊥MM′.
∴MH=M′H=DM′+DH=BM+DH,DM⊥AN.
②Ⅰ.当点C在
 |
| DNM |


同理可得:EF=BE+DF.
Ⅱ.当点C在
 |
| AD |

同理可得:EF=DF-BE.
点评:本题考查了正方形的性质、全等三角形的判定与性质、圆内接四边形的性质、等腰三角形的性质、勾股定理、解一元二次方程等知识,考查了阅读理解能力、自学能力、运用已有经验解决问题的能力,有一定的综合性,是一道好题.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目

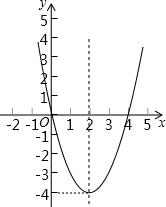 如图,二次函数图象经过原点且顶点坐标为(-4,-2),求该函数解析式.
如图,二次函数图象经过原点且顶点坐标为(-4,-2),求该函数解析式.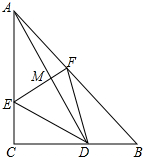 如图,D是等腰直角△ABC的直角边BC上一点,AD的垂直平分线EF分别交AC、AD、AB于E、M、F,BC=2.
如图,D是等腰直角△ABC的直角边BC上一点,AD的垂直平分线EF分别交AC、AD、AB于E、M、F,BC=2.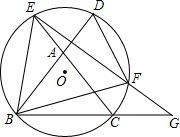 如图,△ABC是等边三角形,⊙O过点B、C,且与BA、CA的延长线分别交于点D、E,弦DF∥AC,EF的延长线交BC的延长线于点G.求证:△BEF是等边三角形.
如图,△ABC是等边三角形,⊙O过点B、C,且与BA、CA的延长线分别交于点D、E,弦DF∥AC,EF的延长线交BC的延长线于点G.求证:△BEF是等边三角形.