题目内容
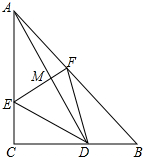 如图,D是等腰直角△ABC的直角边BC上一点,AD的垂直平分线EF分别交AC、AD、AB于E、M、F,BC=2.
如图,D是等腰直角△ABC的直角边BC上一点,AD的垂直平分线EF分别交AC、AD、AB于E、M、F,BC=2.(1)当CD=
| 2 |
(2)当AD平分∠BAC时,四边形AEDF是何种特殊的平行四边形?请证明你的结论,并求出CD的长.
考点:菱形的判定,勾股定理,等腰直角三角形
专题:
分析:(1)设AE=x,则EC=2-x,ED=AE=x,在△ECD中,利用EC2+CD2=ED2列出有关x的方程求得AE的长即可;
(2)首先利用两组对角分别相等的四边形是平行四百那些证得四边形AEDF为平行四边形,然后证得对角线垂直,从而利用对角线互相垂直的平行四边形是菱形即可.
(2)首先利用两组对角分别相等的四边形是平行四百那些证得四边形AEDF为平行四边形,然后证得对角线垂直,从而利用对角线互相垂直的平行四边形是菱形即可.
解答:解:(1)设AE=x,则EC=2-x,ED=AE=x,
在△ECD中,EC2+CD2=ED2,
即:(2-x)2+(
)2=x2,
解得:x=
.
(2)四边形AEDF是菱形,理由如下:
∵:AD平分∠BAC,
∴△AFD为等腰三角形,AE=AF,
∵BAC=45°,
∴∠AEF=∠AFE=67.5°,
∵△AFD和△AED都是等腰三角形,
∴AFD=∠DFM,∠AEF=∠DEF,
∴AFD=135°,∠AED=135°,
∴EDF=45°,
∴四边形AEDF为平行四边形,
∵AD⊥EF,
∴四边形AEDF为菱形;
设CD=x,则BD=AE=2-x,ED=
x,
则
x=2-x,
解得:x=2
-2.
在△ECD中,EC2+CD2=ED2,
即:(2-x)2+(
| 2 |
解得:x=
| 3 |
| 2 |
(2)四边形AEDF是菱形,理由如下:
∵:AD平分∠BAC,
∴△AFD为等腰三角形,AE=AF,
∵BAC=45°,
∴∠AEF=∠AFE=67.5°,
∵△AFD和△AED都是等腰三角形,
∴AFD=∠DFM,∠AEF=∠DEF,
∴AFD=135°,∠AED=135°,
∴EDF=45°,
∴四边形AEDF为平行四边形,
∵AD⊥EF,
∴四边形AEDF为菱形;
设CD=x,则BD=AE=2-x,ED=
| 2 |
则
| 2 |
解得:x=2
| 2 |
点评:本题考查了菱形的判定及勾股定理的应用,解题的关键是从题目中整理出直角三角形,难点是判定菱形.

练习册系列答案
相关题目

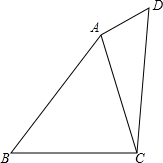 已知:∠B=∠D,∠BCA+∠CAD=180°.求证:AB=CD.
已知:∠B=∠D,∠BCA+∠CAD=180°.求证:AB=CD. 如图,在方格纸上有一小段AB和一点C.
如图,在方格纸上有一小段AB和一点C. 如图所示,AB、CD相交于点O.OB平分∠DOE,若∠DOE=63°12′,则∠AOC的度数是
如图所示,AB、CD相交于点O.OB平分∠DOE,若∠DOE=63°12′,则∠AOC的度数是