题目内容
16.在同一坐标系中,一次函数y=ax+b与二次函数y=ax2+b的大致图象是( )| A. |  | B. |  | C. |  | D. |  |
分析 可先根据一次函数的图象判断a、b的符号,再判断二次函数图象与实际是否相符,判断正误.
解答 解:A、由一次函数y=ax+b的图象可得:a>0,此时二次函数y=ax2+b的图象应该开口向上,故A错误;
B、由一次函数y=ax+b的图象可得:a<0,b>0,此时二次函数y=ax2+b的图象应该开口向下,顶点的纵坐标大于零,故B错误;
C、由一次函数y=ax+b的图象可得:a<0,b>0,此时二次函数y=ax2+b的图象应该开口向下,顶点的纵坐标大于零,故C正确;
D、由一次函数y=ax+b的图象可得:a>0,b>0,此时抛物线y=ax2+b的顶点的纵坐标大于零,故D错误;
故选:C.
点评 本题考查了二次函数的图象,应该熟记一次函数y=kx+b在不同情况下所在的象限,以及熟练掌握二次函数的有关性质:开口方向、对称轴、顶点坐标等.

练习册系列答案
相关题目
4.已知$\frac{a}{b}$=$\frac{2}{3}$,则$\frac{a}{a+b}$的值为( )
| A. | $\frac{5}{3}$ | B. | $\frac{5}{2}$ | C. | $\frac{2}{5}$ | D. | $\frac{3}{5}$ |
11. 如图,已知AB∥CD,∠EBA=50°,∠E+∠D的度数为( )
如图,已知AB∥CD,∠EBA=50°,∠E+∠D的度数为( )
 如图,已知AB∥CD,∠EBA=50°,∠E+∠D的度数为( )
如图,已知AB∥CD,∠EBA=50°,∠E+∠D的度数为( )| A. | 30° | B. | 50° | C. | 60° | D. | 90° |
1.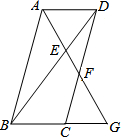 如图,在?ABCD中,G为BC延长线的一点,连结AG交对角线BD于E,交CD于F,下面结论错误的是( )
如图,在?ABCD中,G为BC延长线的一点,连结AG交对角线BD于E,交CD于F,下面结论错误的是( )
 如图,在?ABCD中,G为BC延长线的一点,连结AG交对角线BD于E,交CD于F,下面结论错误的是( )
如图,在?ABCD中,G为BC延长线的一点,连结AG交对角线BD于E,交CD于F,下面结论错误的是( )| A. | $\frac{EA}{EG}$=$\frac{AD}{BG}$ | B. | $\frac{DE}{BE}$=$\frac{FD}{FG}$ | C. | $\frac{CF}{CG}$=$\frac{CD}{BG}$ | D. | $\frac{AD}{BG}$=$\frac{AF}{AG}$ |
8.已知整数a1,a2,a3,a4…满足下列条件:a1=0,a2=-|a1+1|,a3=-|a2+2|,a4=-|a3+3|…依此类推,则a2017的值为( )
| A. | -1009 | B. | -1008 | C. | -2017 | D. | -2016 |
6.$\frac{1}{4}$的算术平方根是( )
| A. | ±$\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{16}$ |