Question

6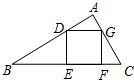．如图，△ABC中∠BAC=90°，正方形DEFG内接于△ABC，且△BDE、△CFG的面积分别为4、1，则△ADG的面积是$\frac{4}{5}$．

Answer 1

分析 根据已知条件得到△DEB∽△CFG，根据相似三角形的性质得到$\frac{{S}_{△BDE}}{{S}_{△CFG}}$=（$\frac{BE}{FG}$）²=$\frac{4}{1}$，得到$\frac{DG}{BE}$=$\frac{1}{2}$，设DG=DE=x，求得BD=$\sqrt{5}$x，通过△ADG∽△EBD，根据相似三角形的性质即可得到结论．

解答 解：∵正方形DEFG内接于△ABC，
∴∠DGF=∠DEF=∠GFE=90°，
∴∠DEB=∠GFC=90°，
∵∠A=90°，
∴∠B+∠C=∠C+∠CGF=90°，
∴∠B=∠CGF，
∴△DEB∽△CFG，
∴$\frac{{S}_{△BDE}}{{S}_{△CFG}}$=（$\frac{BE}{FG}$）²=$\frac{4}{1}$，
∴$\frac{GF}{BE}$=$\frac{1}{2}$，
∴$\frac{DG}{BE}$=$\frac{1}{2}$，
设DG=DE=x，
∴BE=2x，
∴BD=$\sqrt{5}$x，
∵DG∥BC，
∴∠ADG=∠B，
∴△ADG∽△EBD，
∴$\frac{{S}_{△ADG}}{{S}_{△BDE}}$=（$\frac{DG}{BD}$）²=$\frac{4}{5}$，
故答案为：$\frac{4}{5}$．

点评 本题考查了相似三角形的性质和判定，三角形面积公式，正方形的性质的应用，注意：相似三角形的面积比等于相似比的平方．